7.下列函数中,周期为1的奇函数是( )
| A. | y=cos2πx | B. | y=sinπxcosπx | C. | $y=tan\frac{π}{2}x$ | D. | $y=sin(2πx+\frac{π}{3})$ |
5.下列说法中正确的是( )
| A. | 一个命题的逆命题为真,则它的逆否命题一定为真 | |
| B. | 若“ac2>bc2”,则a>b | |
| C. | ?x0∈R,$sin{x_0}+cos{x_0}=\frac{3}{2}$ | |
| D. | “a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0” |
4.等比数列{an}中,a1+a4+a7=3,a3+a6+a9=27,则数列{an}前9项的和S9等于( )
| A. | 39 | B. | 21 | C. | 39或21 | D. | 21或36 |
1.某中学有篮球社,吉他社,传统文化社,动漫社等多个社团,其中传统文化社借端午节来临之际举行包粽子送祝福活动,随机调查了高三50名男女生对粽子口味的喜好,统计如下表:
(1)按以上统计数据填写下面的2×2列联表,并运用独立性检验思想,判断是否有97.5%把握认为甜味粽和咸味粽的喜好与性别有关系?
参考公式及临界值表如下:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
(2)从被调查的50人中对玫瑰粽和什锦粽喜好的同学按照分层抽样的方法抽取4名同学按顺序进行深度调查,则前两位接受调查的都是喜好玫瑰粽同学的概率是多少?
| 甜味粽 | 咸味粽 | 南国风味 | ||||
| 枣子粽 | 豆沙粽 | 玫瑰粽 | 蛋黄粽 | 猪肉粽 | 什锦粽 | |
| 男生 | 4 | 3 | 1 | 10 | 4 | 3 |
| 女生 | 6 | 5 | 5 | 5 | 1 | 3 |
| 甜味粽 | 咸味粽 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
18.直线l1:ax+y-a+1=0,直线l1:4x+ay-2=0,则“a=±2”是“l1∥l2”的( )
0 239856 239864 239870 239874 239880 239882 239886 239892 239894 239900 239906 239910 239912 239916 239922 239924 239930 239934 239936 239940 239942 239946 239948 239950 239951 239952 239954 239955 239956 239958 239960 239964 239966 239970 239972 239976 239982 239984 239990 239994 239996 240000 240006 240012 240014 240020 240024 240026 240032 240036 240042 240050 266669
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 不充分不必要条件 |
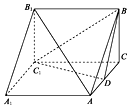 如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=2,D为AC的中点.
如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=2,D为AC的中点.