12.某车间需要确定加工零件的加工时间,进行了若干次试验.根据收集到的数据(如表):
由最小二乘法求得回归直线方程$\hat y=0.67x+\hat a$,则$\hat a$的值为54.9.
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 68 | 75 | 81 | 89 |
11.某三棱锥的三视图如图所示,正视图和俯视图都是等腰直角三角形,则该三棱锥中棱长最大值是( )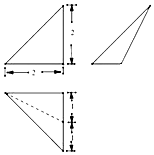

| A. | $2\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{5}$ |
7.执行如图所示的程序框图,若输出的结果是$\frac{99}{199}$,则判断框内应填的内容是( )


| A. | n≤97 | B. | n≤98 | C. | n≤99 | D. | n≤100 |
6.已知在三角形ABC中,AB<AC,∠BAC=90°,边AB,AC的长分别为方程${x^2}-2({1+\sqrt{3}})x+4\sqrt{3}=0$的两个实数根,若斜边BC上有异于端点的E,F两点,且EF=1,∠EAF=θ,则tanθ的取值范围为( )
| A. | $({\frac{{\sqrt{3}}}{3},\frac{{4\sqrt{3}}}{11}}]$ | B. | $({\frac{{\sqrt{3}}}{9},\frac{{\sqrt{3}}}{3}})$ | C. | $({\frac{{\sqrt{3}}}{9},\frac{{4\sqrt{3}}}{11}}]$ | D. | $({\frac{{\sqrt{3}}}{9},\frac{{2\sqrt{3}}}{11}}]$ |
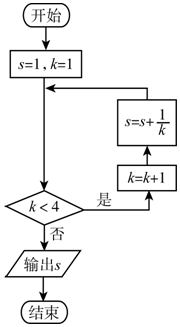
5.执行如图所示的程序框图,则输出的s值为( )
0 239760 239768 239774 239778 239784 239786 239790 239796 239798 239804 239810 239814 239816 239820 239826 239828 239834 239838 239840 239844 239846 239850 239852 239854 239855 239856 239858 239859 239860 239862 239864 239868 239870 239874 239876 239880 239886 239888 239894 239898 239900 239904 239910 239916 239918 239924 239928 239930 239936 239940 239946 239954 266669

| A. | $\frac{11}{6}$ | B. | $\frac{13}{6}$ | C. | $\frac{25}{12}$ | D. | $\frac{29}{12}$ |
 把正整数按一定的规律排成如图所示的三角形数阵.设aij(i,j∈N*)是位于数阵中从上向下数第i行,从左向右数第j列的数,例如:a43=10,若aij=173,则i+j=11.
把正整数按一定的规律排成如图所示的三角形数阵.设aij(i,j∈N*)是位于数阵中从上向下数第i行,从左向右数第j列的数,例如:a43=10,若aij=173,则i+j=11.