题目内容
9.已知在△ABC中,a,b,c分别是角A,B,C所对应的边,且a-2b=0.(1)若$B=\frac{π}{6}$,求C;
(2)若$C=\frac{2}{3}π,c=14$,求△ABC的面积.
分析 (1)由已知得sinA=2sinB=1,即$A=\frac{π}{2}$,$C=π-A-B=\frac{π}{3}$.
(2)由题意,由余弦定理得a、b,即可求得△ABC的面积.
解答 解:(1)∵$B=\frac{π}{6},a-2b=0$,∴sinA=2sinB=1,
又∵0<A<π,∴$A=\frac{π}{2}$,∴$C=π-A-B=\frac{π}{3}$.
(2)由题意,由余弦定理得142=b2+4b2-2$•b•2b•cos\frac{2π}{3}$,∴$b=2\sqrt{7},a=4\sqrt{7}$,
∴${S_{△ABC}}=\frac{1}{2}absinC=14\sqrt{3}$.
点评 本题考查了三角形中的求值,余弦定理,三角形的面积计算,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
17.如果执行下面的框图,当m=7,n=3时,输出的S值为( )
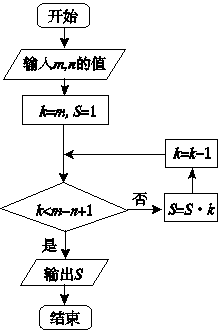

| A. | 7 | B. | 42 | C. | 210 | D. | 840 |
18.已知(1)正方形的对角线相等;(2)平行四边形的对角线相等;(3)正方形是平行四边形.由(1)、(2)、(3)组合成“三段论”,根据“三段论”推理出一个结论,则这个结论是( )
| A. | 正方形是平行四边形 | B. | 平行四边形的对角线相等 | ||
| C. | 正方形的对角线相等 | D. | 以上均不正确 |
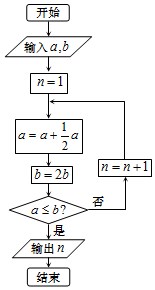 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为5和2,则输出的n=4.
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为5和2,则输出的n=4.