题目内容
10.已知直线l的参数方程为$\left\{\begin{array}{l}x=m+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.(t$为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,椭圆C的极坐标方程为$5{cos^2}θ+9{sin^2}θ=\frac{45}{ρ^2}$,且直线l经过椭圆C的右焦点F.(1)求椭圆C的内接矩形PMNQ面积的最大值;
(2)若直线l与椭圆C交于A,B两点,求|FA|•|FB|的值.
分析 (1)将椭圆的极坐标方程转化成标准方程,设P点坐标,根据二倍角公式及正弦函数的性质,即可求得椭圆C的内接矩形PMNQ面积的最大值;
(2)将参数方程代入椭圆的标准方程,由韦达定理即可求得${t_1}{t_2}=-\frac{25}{8}$,即可求得|FA|•|FB|的值.
解答 解:(1)椭圆C化为5ρ2cos2θ+9ρ2sin2θ=45,∴5x2+9y2=45,
∴椭圆的标准方程:$\frac{x^2}{9}+\frac{y^2}{5}=1$.设椭圆C的内接矩形PMNQ中,P的坐标为$({3cosα,\sqrt{5}sinα})$,
∴${S_{PMNQ}}=|{4×3cosα×\sqrt{5}sinα}|=|{12\sqrt{5}sinαcosα}|=6\sqrt{5}|{sin2α}|≤6\sqrt{5}$.
∴椭圆C的内接矩形PMNQ面积最大值为$6\sqrt{5}$.
(2)由椭圆C的方程$\frac{x^2}{9}+\frac{y^2}{5}=1$,得椭圆C的右焦点F(2,0),由直线l经过右焦点F(2,0),得m=2,
易得直线l的参数方程可化为$\left\{\begin{array}{l}x=2+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.(t$为参数),代入到5x2+9y2=45,整理得,8t2+10t-25=0,
∴${t_1}{t_2}=-\frac{25}{8}$,即$|{FA}|•|{FB}|=\frac{25}{8}$.
|FA|•|FB|的值$\frac{25}{8}$.
点评 本题考查椭圆的极坐标与直角坐标的转化,直线与椭圆的位置关系,考查韦达定理,二倍角公式,考查计算能力,属于中档题.

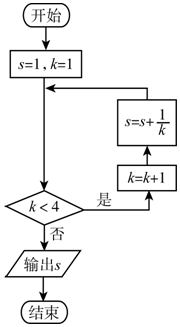
| A. | $\frac{11}{6}$ | B. | $\frac{13}{6}$ | C. | $\frac{25}{12}$ | D. | $\frac{29}{12}$ |
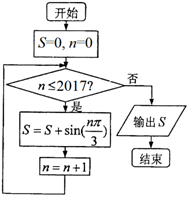
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | 0 | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
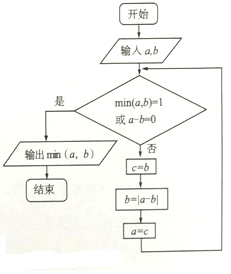 min(a,b)表示a,b中的最小值,执行如图所示的程序框图,若输入的a,b值分别为4,10,则输出的min(a,b)值是( )
min(a,b)表示a,b中的最小值,执行如图所示的程序框图,若输入的a,b值分别为4,10,则输出的min(a,b)值是( )