题目内容
12.某车间需要确定加工零件的加工时间,进行了若干次试验.根据收集到的数据(如表):| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 68 | 75 | 81 | 89 |
分析 计算$\overline{x}$、$\overline{y}$,根据回归直线方程过样本中心点($\overline{x}$,$\overline{y}$),求出$\hat a$的值.
解答 解:计算$\overline{x}$=$\frac{1}{5}$×(10+20+30+40+50)=30,
$\overline{y}$=$\frac{1}{5}$×(62+68+75+81+89)=75,
回归直线方程$\hat y=0.67x+\hat a$过样本中心点($\overline{x}$,$\overline{y}$),
∴$\hat a$=$\overline{y}$-0.67$\overline{x}$=75-0.67×30=54.9.
故答案为:54.9.
点评 本题考查了回归直线方程过样本中心点的应用问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}$,$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$,$\sqrt{4+\frac{4}{15}}=4\sqrt{\frac{4}{15}}$,…,$\sqrt{m+\frac{m}{t}}=m\sqrt{\frac{m}{t}}$(m,t∈N*且m≥2),若不等式λm-t-3<0恒成立,则实数λ的取值范围为( )
| A. | $[2\sqrt{2},+∞)$ | B. | $(-∞,2\sqrt{2})$ | C. | (-∞,3) | D. | [1,3] |
3.运行如图所示的程序框图,输出的S值等于$\frac{{{2^{10}}-1}}{{{2^{10}}}}$,则判断框内可以填( )
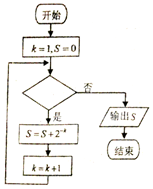

| A. | k≤8? | B. | k≤9? | C. | k≤10? | D. | k≤11? |
7.执行如图所示的程序框图,若输出的结果是$\frac{99}{199}$,则判断框内应填的内容是( )


| A. | n≤97 | B. | n≤98 | C. | n≤99 | D. | n≤100 |
1.如图的程序框图,其作用是输入x的值,输出相应的y值,若x=y,则这样的x值有( )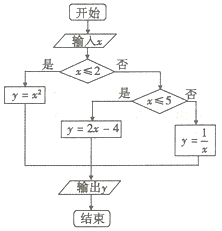

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |