题目内容
11.某三棱锥的三视图如图所示,正视图和俯视图都是等腰直角三角形,则该三棱锥中棱长最大值是( )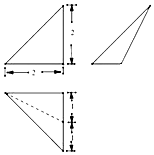
| A. | $2\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{5}$ |
分析 由三视图可知:该几何体为三棱锥,P-ABC,其中侧面PAB⊥底面ABC,底面ABC为直角三角形,AB⊥BC,BC=2,AB=1,在平面OAB内,过点P作PO⊥AB,垂足为O,则PO⊥底面ABC,PO=2,AO=1.则该三棱锥中最长的棱长为PC.
解答  解:由三视图可知:该几何体为三棱锥,P-ABC,
解:由三视图可知:该几何体为三棱锥,P-ABC,
其中侧面PAB⊥底面ABC,底面ABC为直角三角形,
AB⊥BC,BC=2,AB=1,在平面OAB内,
过点P作PO⊥AB,垂足为O,则PO⊥底面ABC,PO=2,AO=1.
则该三棱锥中最长的棱长为
PC=$\sqrt{P{O}^{2}+O{C}^{2}}$=$\sqrt{P{O}^{2}+B{C}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+2×{2}^{2}}$=2$\sqrt{3}$.
故选:B.
点评 本题考查了三棱锥的三视图、勾股定理、位置关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.某木材加工流程图如图所示,则木材在封底漆之前需要经过的工序有( )


| A. | 9道 | B. | 8道 | C. | 7道 | D. | 6道 |
19.若曲线C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=1+2sinθ\end{array}\right.$(参数$θ∈[{-\frac{π}{2},\frac{π}{2}}]$),则曲线C( )
| A. | 表示直线 | B. | 表示线段 | C. | 表示圆 | D. | 表示半个圆 |
6.已知在三角形ABC中,AB<AC,∠BAC=90°,边AB,AC的长分别为方程${x^2}-2({1+\sqrt{3}})x+4\sqrt{3}=0$的两个实数根,若斜边BC上有异于端点的E,F两点,且EF=1,∠EAF=θ,则tanθ的取值范围为( )
| A. | $({\frac{{\sqrt{3}}}{3},\frac{{4\sqrt{3}}}{11}}]$ | B. | $({\frac{{\sqrt{3}}}{9},\frac{{\sqrt{3}}}{3}})$ | C. | $({\frac{{\sqrt{3}}}{9},\frac{{4\sqrt{3}}}{11}}]$ | D. | $({\frac{{\sqrt{3}}}{9},\frac{{2\sqrt{3}}}{11}}]$ |
3.($\sqrt{x}$-$\frac{1}{x}$)9展开式中的常数项是( )
| A. | -84 | B. | 84 | C. | -36 | D. | 36 |