Question

5．执行如图所示的程序框图，则输出的s值为（　　）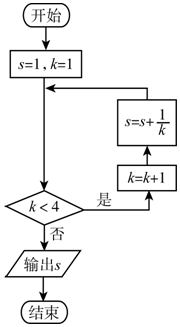

• A． $\frac{11}{6}$
• B． $\frac{13}{6}$
• C． $\frac{25}{12}$
• D． $\frac{29}{12}$

Answer 1

分析 模拟执行程序框图，依次写出每次循环得到的s，k的值，当k=4时不满足条件k＜4，退出循环，输出S的值即可得解．

解答 解：模拟执行程序框图，可得
s=1，k=1
满足条件k＜4，执行循环体，k=2，s=1+$\frac{1}{2}$
满足条件k＜4，执行循环体，k=3，s=1+$\frac{1}{2}$+$\frac{1}{3}$
满足条件k＜4，执行循环体，k=4，s=1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$
不满足条件k＜4，退出循环，输出s的值为s=1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$=$\frac{25}{12}$．
故选：C．

点评 本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．