1.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左,右焦点分别是F1,F2,点P在双曲线上,且满足∠PF2F1=2∠PF1F2=60°,则此双曲线的离心率等于( )
| A. | 2$\sqrt{3}$-2 | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{3}$+1 | D. | 2$\sqrt{3}$+2 |
19.若曲线C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=1+2sinθ\end{array}\right.$(参数$θ∈[{-\frac{π}{2},\frac{π}{2}}]$),则曲线C( )
| A. | 表示直线 | B. | 表示线段 | C. | 表示圆 | D. | 表示半个圆 |
17.如果执行下面的框图,当m=7,n=3时,输出的S值为( )
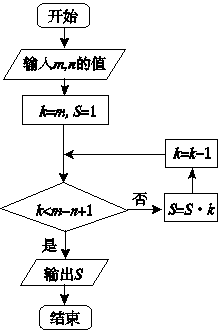

| A. | 7 | B. | 42 | C. | 210 | D. | 840 |
15.《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题,《数书九章》中记录了秦九昭的许多创造性成就,其中在卷五“三斜求职”中提出了已知三角形三边a,b,c求面积的公式,这与古希腊的海伦公式完成等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.”若把以上这段文字写成公式,即S=$\sqrt{\frac{1}{4}[{c^2}{a^2}-{{(\frac{{{c^2}+{a^2}-{b^2}}}{2})}^2}]}$,现有周长为10+2$\sqrt{7}$的△ABC满足sinA:sinB:sinC=2:3:$\sqrt{7}$,则用以上给出的公式求得△ABC的面积为( )
0 239759 239767 239773 239777 239783 239785 239789 239795 239797 239803 239809 239813 239815 239819 239825 239827 239833 239837 239839 239843 239845 239849 239851 239853 239854 239855 239857 239858 239859 239861 239863 239867 239869 239873 239875 239879 239885 239887 239893 239897 239899 239903 239909 239915 239917 239923 239927 239929 239935 239939 239945 239953 266669
| A. | $6\sqrt{3}$ | B. | $4\sqrt{7}$ | C. | $8\sqrt{7}$ | D. | 12 |
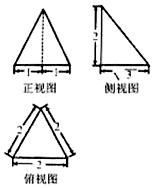 某几何体的三视图如图所示,则该几何体最长的一条棱的长度=2$\sqrt{2}$,体积为$\frac{2\sqrt{3}}{3}$.
某几何体的三视图如图所示,则该几何体最长的一条棱的长度=2$\sqrt{2}$,体积为$\frac{2\sqrt{3}}{3}$.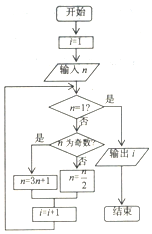 20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )
20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )