题目内容
2.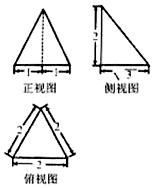 某几何体的三视图如图所示,则该几何体最长的一条棱的长度=2$\sqrt{2}$,体积为$\frac{2\sqrt{3}}{3}$.
某几何体的三视图如图所示,则该几何体最长的一条棱的长度=2$\sqrt{2}$,体积为$\frac{2\sqrt{3}}{3}$.
分析 如图所示,该几何体为三棱锥P-ABC.其中PA⊥底面ABC,PA=2,底面△ABC是边长为2的等边三角形.
解答 解:如图所示,该几何体为三棱锥P-ABC.其中PA⊥底面ABC,PA=2,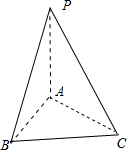
底面△ABC是边长为2的等边三角形.
该几何体最长的一条棱的长度为PA或PC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
体积V=$\frac{1}{3}×\frac{\sqrt{3}}{4}×{2}^{2}×2$=$\frac{2\sqrt{3}}{3}$.
故答案为:2$\sqrt{2}$,$\frac{2\sqrt{3}}{3}$.
点评 本题考查了三棱锥的三视图、体积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
12.把-1485°化为α+2kπ(k∈Z,0≤α≤2π)的形式是( )
| A. | $\frac{π}{4}$-8π | B. | -$\frac{7}{4}$π-8π | C. | -$\frac{π}{4}$-10π | D. | -10π+$\frac{7π}{4}$ |
13.若直线x-y-2=0被圆(x-a)2+y2=4所截得的弦长为$2\sqrt{2}$,则实数a为( )
| A. | -1或$\sqrt{3}$ | B. | 1或3 | C. | -2或6 | D. | 0或4 |
17.如果执行下面的框图,当m=7,n=3时,输出的S值为( )
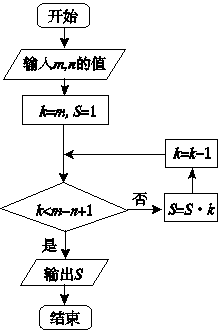

| A. | 7 | B. | 42 | C. | 210 | D. | 840 |
7.执行如图所示的程序框图,若输出的结果是$\frac{99}{199}$,则判断框内应填的内容是( )


| A. | n≤97 | B. | n≤98 | C. | n≤99 | D. | n≤100 |
12.第17届亚运会于2014年9月19日至10月4日在韩国仁川进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下2×2列联表:
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有4人会外语),抽取2名负责翻译工作,那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少?参考公式:K2=$\frac{n(ad-b{c)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
(1)根据以上数据完成以下2×2列联表:
| 喜爱运 动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
(3)如果从喜欢运动的女志愿者中(其中恰有4人会外语),抽取2名负责翻译工作,那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少?参考公式:K2=$\frac{n(ad-b{c)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
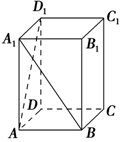 如图所示,在长方体ABCD-A1B1C1D1中,AA1=2AB=2BC,求异面直线A1B与AD1所成角的余弦值.
如图所示,在长方体ABCD-A1B1C1D1中,AA1=2AB=2BC,求异面直线A1B与AD1所成角的余弦值.