题目内容
18．在极坐标系中，射线θ=$\frac{π}{4}$被圆ρ=4sinθ截得的弦长为2$\sqrt{2}$．分析 把θ=$\frac{π}{4}$代入圆ρ=4sinθ，可得截得的弦长．
解答 解：把θ=$\frac{π}{4}$代入圆ρ=4sinθ，可得$ρ=4sin\frac{π}{4}$=2$\sqrt{2}$．
因此截得的弦长为2$\sqrt{2}$．
故答案为：$2\sqrt{2}$．
点评 本题考查了极坐标方程的应用、直线与圆相交弦长问题，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
8．函数$y=sin（x+\frac{π}{4}）$在闭区间（ ）上为增函数．
| A． | $[-\frac{3}{4}π，\frac{π}{4}]$ | B． | [-π，0] | C． | $[-\frac{π}{4}，\frac{3}{4}π]$ | D． | $[-\frac{π}{2}，\frac{π}{2}]$ |
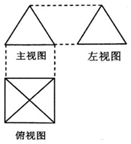如图，一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形，其俯视图轮廓为正方形，则其体积是$\frac{4\sqrt{3}}{3}$，表面积为12．
13．
执行如图所示的程序框图，如果输入的m=15，n=12，则输出的n是（ ）
执行如图所示的程序框图，如果输入的m=15，n=12，则输出的n是（ ）| A． | 15 | B． | 12 | C． | 3 | D． | 180 |