题目内容
3．已知实数x，y满足x2+y2-6x+8y-11=0，则$\sqrt{{x}^{2}+{y}^{2}}$的最大值=11，|3x+4y-28|的最小值=5．分析 化圆的一般方程为标准方程，可得x-3=6cosθ，y+4=6sinθ，分别代入$\sqrt{{x}^{2}+{y}^{2}}$与|3x+4y-28|，然后利用辅助角公式化简求最值．
解答 解：化方程x2+y2-6x+8y-11=0为（x-3）2+（y+4）2=36．
令x-3=6cosθ，y+4=6sinθ，
则x=3+6cosθ，y=-4+6sinθ，
∴$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{（3+6cosθ）^{2}+（-4+6sinθ）^{2}}$=$\sqrt{61+60cos（θ+α）}$（tanα=$\frac{4}{3}$）．
∴$\sqrt{{x}^{2}+{y}^{2}}$的最大值为$\sqrt{121}=11$；
|3x+4y-28|=|9+18cosθ-16+24sinθ-28|=|24sinθ+18cosθ-35|=|30sin（θ+β）-35|（tanβ=$\frac{3}{4}$）．
∴|3x+4y-28|的最小值为|30-35|=5．
故答案为：11，5．
点评 本题考查化圆的一般方程为标准方程，考查圆的参数方程的应用，训练了利用辅助角公式求三角函数的最值，是中档题．
练习册系列答案
相关题目
把正整数按一定的规律排成如图所示的三角形数阵．设aij（i，j∈N*）是位于数阵中从上向下数第i行，从左向右数第j列的数，例如：a43=10，若aij=173，则i+j=11．
15．执行如图所示的程序框图，输出的S值为（ ）
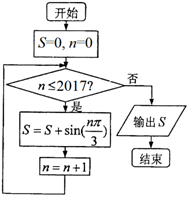
| A． | $-\frac{{\sqrt{3}}}{2}$ | B． | 0 | C． | $\sqrt{3}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
一个均速旋转的摩天轮每12分钟逆时针旋转一周，最低点距地面2米，最高点距地面18米，甲从摩天轮最低点处上摩天轮，3分钟后乙也在其最低点处上摩天轮，从乙上摩天轮开始计时，在摩天轮转动的一圈内，有3分钟，甲、乙距地面的高度之和不小于28米．