题目内容
20.在△ABC中,角A,B,C的对边分别为a,b,c,已知$\frac{a}{c}$cosB+$\frac{b}{c}$cosA=$\frac{\sqrt{3}}{2cosC}$( I)求∠C的大小;
( II)求sinB-$\sqrt{3}$sinA的最小值.
分析 (I)由正弦定理,得 $\frac{sin(A+B)}{sinC}=\frac{\sqrt{3}}{2cosC}$.即cosC=$\frac{\sqrt{3}}{2}$,可得C=$\frac{π}{6}$.
(II)sinB-$\sqrt{3}$sinA=sin($\frac{5π}{6}-A$)-$\sqrt{3}$sinA$\frac{1}{2}cosA-\frac{\sqrt{3}}{2}sinA$=cos(A+$\frac{π}{3}$)
由A+B=$\frac{5π}{6}$,得A+$\frac{π}{3}$$∈(\frac{π}{3},\frac{7π}{6})$,cos(A+$\frac{π}{3}$)最小值为-1.即可得sinB-$\sqrt{3}$sinA的最小值
解答 解:(I)由正弦定理,得 $\frac{a}{c}=\frac{sinA}{sinC}$,$\frac{b}{c}=\frac{sinB}{sinC}$.
所以,$\frac{sinAcosB+cosAsinB}{sinC}=\frac{\sqrt{3}}{2cosC}$,即$\frac{sin(A+B)}{sinC}=\frac{\sqrt{3}}{2cosC}$.
∵A+B+C=π,∴sin(A+B)=sinC.
∴2cosC=$\sqrt{3}$,cosC=$\frac{\sqrt{3}}{2}$
∵C∈(0,π),∴C=$\frac{π}{6}$.
( II)∵A+B+C=π∴A+B=$\frac{5π}{6}$
∴sinB-$\sqrt{3}$sinA=sin($\frac{5π}{6}-A$)-$\sqrt{3}$sinA=$\frac{1}{2}cosA-\frac{\sqrt{3}}{2}sinA$=cos(A+$\frac{π}{3}$),
∵A+B=$\frac{5π}{6}$,∴A$∈(0,\frac{5π}{6})$,∴A+$\frac{π}{3}$$∈(\frac{π}{3},\frac{7π}{6})$
∴cos(A+$\frac{π}{3}$)最小值为-1.即sinB-$\sqrt{3}$sinA的最小值为-1.
点评 本题考查了三角恒等变形、正余弦定理的应用,属于中档题.

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案| A. | 点P必在直线AC上 | B. | 点P必在直线BD上 | ||
| C. | 点P必在平面DBC内 | D. | 点P必在平面ABC外 |
| A. | $6\sqrt{3}$ | B. | $4\sqrt{7}$ | C. | $8\sqrt{7}$ | D. | 12 |
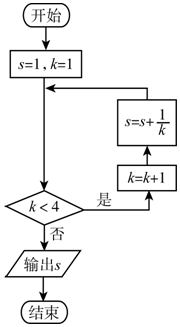
| A. | $\frac{11}{6}$ | B. | $\frac{13}{6}$ | C. | $\frac{25}{12}$ | D. | $\frac{29}{12}$ |
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 68 | 75 | 81 | 89 |