18.曲线y=x•ex在x=1处切线的斜率等于( )
| A. | 2e | B. | e | C. | 2 | D. | 1 |
16.△ABC是底边边长为2$\sqrt{2}$的等腰直角三角形,P是以直角顶点C为圆心,半径为1的圆上任意一点,若m≤$\overrightarrow{AP}$•$\overrightarrow{PB}$≤n,则n-m的最小值为( )
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
15.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左焦点为F,若点F关于直线$y=-\frac{1}{2}x$的对称点P在椭圆C上,则椭圆C的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{5}}}{3}$ |
14.已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-$\frac{π}{2}$≤φ<$\frac{π}{2}$)的图象关于直线x=$\frac{π}{3}$对称,且图象上相邻最高点的距离为π.将函数y=f(x)的图象向右平移$\frac{π}{12}$个单位后,得到y=g(x)的图象,则g(x)的单调递减区间为.
| A. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | B. | [kπ-$\frac{5π}{12}$,kπ-$\frac{11π}{12}$],k∈Z | ||
| C. | [kπ-$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | D. | [kπ+$\frac{5π}{12}$,kπ-$\frac{11π}{12}$],k∈Z |
11.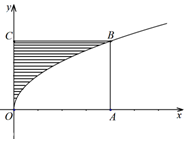 如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
0 239696 239704 239710 239714 239720 239722 239726 239732 239734 239740 239746 239750 239752 239756 239762 239764 239770 239774 239776 239780 239782 239786 239788 239790 239791 239792 239794 239795 239796 239798 239800 239804 239806 239810 239812 239816 239822 239824 239830 239834 239836 239840 239846 239852 239854 239860 239864 239866 239872 239876 239882 239890 266669
 如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )| A. | 2 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
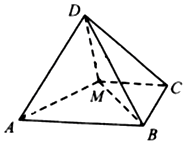 如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM. 四棱锥P-ABCD,侧面PCD为边长为2的正三角形,底面ABCD为对角线互相垂直的等腰梯形,M为AD的中点,$PO=\sqrt{2}$.
四棱锥P-ABCD,侧面PCD为边长为2的正三角形,底面ABCD为对角线互相垂直的等腰梯形,M为AD的中点,$PO=\sqrt{2}$. 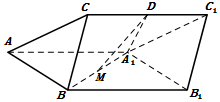 如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.