题目内容
12.设不等式组$\left\{{\begin{array}{l}{2x+y≥2}\\{x-2y≥-4}\\{3x-y≤3}\end{array}}\right.$所表示的平面区域为M,若函数y=k(x+1)+1的图象经过区域M,则实数k的取值范围是$[-\frac{1}{2},1]$.分析 首先画出可行域,利用目标函数的几何意义求最值.
解答  解:不等式组表示的平面区域如图:函数y=k(x+1)+1的图象为经过定点B(-1,1)的直线,要使此直线经过区域M,则斜率kAB≤k≤kBC,其中${k}_{AB}=-\frac{1}{2}$,${k}_{BC}=\frac{2-1}{1}=1$,所以实数k的取值范围是$[-\frac{1}{2},1]$;
解:不等式组表示的平面区域如图:函数y=k(x+1)+1的图象为经过定点B(-1,1)的直线,要使此直线经过区域M,则斜率kAB≤k≤kBC,其中${k}_{AB}=-\frac{1}{2}$,${k}_{BC}=\frac{2-1}{1}=1$,所以实数k的取值范围是$[-\frac{1}{2},1]$;
故答案为:$[-\frac{1}{2},1]$.
点评 本题考查了简单线性规划问题;利用了数形结合的思想,关键是正确画出可行域,利用目标函数的几何意义求最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知函数f(x)的图象关于(1,1)对称,当x∈(0,1]时,f(x)=x2,当x∈(-1,0]时,f(x)+2=$\frac{2}{f(\sqrt{x+1})}$,若g(x)=f(x)-t(x+1)为定义在(-1,3)上的函数,则关于g(x)的零点个数的叙述中错误的是( )
| A. | g(x)可能没有零点 | B. | g(x)可能有1个零点 | C. | g(x)可能有2个零点 | D. | g(x)可能有3个零点 |
3.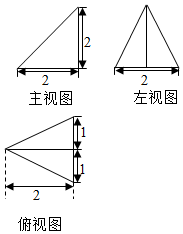 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )
 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得出这个几何体的内切球半径是( )| A. | $\frac{4}{3}$ | B. | $\frac{4}{9}$ | C. | $\sqrt{6}-2$ | D. | $3\sqrt{6}-6$ |
20.已知数列{an}的前n项和是Sn,则下列四个命题中,错误的是( )
| A. | 若数列{an}是公差为d的等差数列,则数列{$\frac{{S}_{n}}{n}$}的公差为$\frac{d}{2}$的等差数列 | |
| B. | 若数列{$\frac{{S}_{n}}{n}$}是公差为d的等差数列,则数列{an}是公差为2d的等差数列 | |
| C. | 若数列{an}是等差数列,则数列的奇数项,偶数项分别构成等差数列 | |
| D. | 若数列{an}的奇数项,偶数项分别构成公差相等的等差数列,则{an}是等差数列 |
4.已知$α∈(0,\frac{π}{2})$,且$2cos2α=cos(α-\frac{π}{4})$,则sin2α的值为( )
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $-\frac{7}{8}$ | D. | $\frac{7}{8}$ |
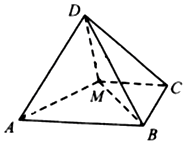 如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.