题目内容
17.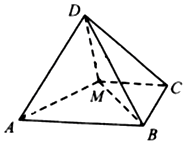 如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.(Ⅰ)证明:AD⊥BD;
(Ⅱ)若AD=DM,
(i)求直线BD与平面AMD所成角的正弦值;
(ii)求三棱锥D-MBC的体积.
分析 (I)由勾股定理得出BM⊥AM,故BM⊥平面ADM,得出BM⊥AD,结合AD⊥DM得出AD⊥平面BDM,从而有AD⊥BD;
(II)(i)由BM⊥平面ADM可知∠BDM为所求角,利用勾股定理求出DM,BM,BD,即可得出结论;
(ii)取AM中点E,连结DE,则可证DE⊥平面ABCM,求出DE,代入体积公式计算即可.
解答 (I)证明:∵四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,
∴$AM=BM=2\sqrt{2}$,
又AB=4,∴AM2+BM2=AB2,∴AM⊥BM.
∵面AMD⊥面ABCM,面AMD∩面ABCM=AM,BM?面ABCM,
∴BM⊥面ADM,∵AD?面ADM
∴BM⊥AD.
∵AD⊥DM,DM∩BM=M,DM?面BDM,BM?面BDM,
∴AD⊥面BDM,∵BD?面BDM,
∴AD⊥BD.
(II)解:(i)由(I)知BM⊥面AMD,
∴∠BDM即为直线BD与平面AMD所成角,
∵△ADM是等腰直角三角形,AM=2$\sqrt{2}$,
∴DM=2,∴BD=$\sqrt{B{M}^{2}+D{M}^{2}}$=2$\sqrt{3}$,
∴$sin∠BDM=\frac{BM}{BD}=\frac{{2\sqrt{2}}}{{2\sqrt{3}}}=\frac{{\sqrt{6}}}{3}$.
(ii)取AM中点E,连结DE,
∵AD=DM,则DE⊥AM,
∵面AMD⊥面ABCM,面AMD∩面ABCM=AM,DE?面AMD,
∴DE⊥面ABCM,
∵DE=$\frac{1}{2}$AM=$\sqrt{2}$,
∴${V_{D-MBC}}=\frac{1}{3}{S_{△MBC}}•DE=\frac{1}{3}×(\frac{1}{2}×2×2)×\sqrt{2}=\frac{{2\sqrt{2}}}{3}$.
点评 本题考查了线面垂直的判定与性质,面面垂直的性质,棱锥的体积计算,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{π}$ | D. | $\frac{π}{16}$ |
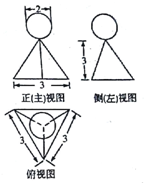 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{4π}{3}$+$\frac{9\sqrt{3}}{4}$ | B. | $\frac{4π}{3}$+$\frac{27\sqrt{3}}{4}$ | C. | $\frac{8π}{3}$+$\frac{9\sqrt{3}}{4}$ | D. | $\frac{8π}{3}$+$\frac{27\sqrt{3}}{4}$ |
| A. | b<0 | B. | b≤0 | C. | b<1 | D. | b≤1 |
 已知f(x)=Asin (ω x+φ)+(A>0,ω>0,|φ|<π})的图象如图所示,则f(3π)=( )
已知f(x)=Asin (ω x+φ)+(A>0,ω>0,|φ|<π})的图象如图所示,则f(3π)=( )| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |