16．已知服从正态分布N(μ.σ2)的随机变量.在区间.和内取值的概率分别为68.27%.95.45%和99.73%.某中学为10000名员工定制校服.设学生的身高服从正态分布N.则适合身高在158-——青夏教育精英家教网——

16．已知服从正态分布N（μ，σ²）的随机变量，在区间（μ-σ，μ+σ），（μ-2σ，μ+2σ）和（μ-3σ，μ+3σ）内取值的概率分别为68.27%，95.45%和99.73%，某中学为10000名员工定制校服，设学生的身高（单位：cm）服从正态分布N（173，25），则适合身高在158～188cm范围内学生穿的校服大约要定制9973套．

15．某班主任对班级90名学生进行了作业量多少的调查，结合数据建立了下列列联表：

	认为作业多	认为作业少	总计
喜欢玩电脑游戏	10	35	45
不喜欢玩玩电脑游戏	7	38	45
总计	17	73	90

利用独立性检验估计，你认为推断喜欢电脑游戏与认为作业多少有关系错误的概率介于（　　）
（观测值表如下）

P（K²≥k₀）	0.50	0.40	0.25	0.15
k₀	0.455	0.708	1.323	2.072

14．设随机变量X～N（2，5²），且P（X≤0）=P（X≥a-2），则实数a的值为（　　）

13．已知某条曲线的参数方程是$\left\{\begin{array}{l}x=2（t+\frac{1}{t}）\\ y=2（t-\frac{1}{t}）\end{array}$（t是参数），则该曲线是（　　）

12．已知圆心在x轴上的圆C与直线l：4x+3y-6=0切于点$M（{\frac{3}{5}，\frac{6}{5}}）$．
（1）求圆C的标准方程；
（2）已知N（2，1），经过原点，且斜率为正数的直线m与圆C交于P（x₁，y₁），Q（x₂，y₂）两点，若|PN|²+|QN|²=24，求直线m的方程．

11．观察数表：

1	2	3	4	…第一行
2	3	4	5	…第二行
3	4	5	6	…第三行
4	5	6	7	…第四行
第一列	第二列	第三列	第四列

根据数表中所反映的规律，第n+1行与第m列的交叉点上的数应该是m+n．

10．已知集合A={-1，0，1}，B={-1，1}，则集合C={a+b|a∈A，b∈B}中的元素个数为（　　）

9．某学校高三年级有学生500人，其中男生300名，女生200名，为了研究学生的数学成绩（单位：分）是否与性别有关，现采用分层抽样的方法，从中抽取了100名学生，先统计了他们期中考试的数学成绩，然后按性别分为男、女两组，再将两组学生的数学成绩分成5组，分别加以统计，得到如图所示的频率分布直方图．

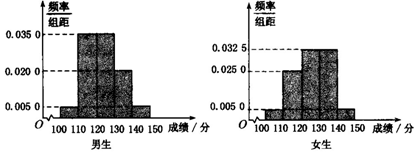
（1）从样本中数学成线小于110分的学生中随机抽取2名学生，求2名学生恰好为一男一女的概率；
（2）若规定数学成绩不小于130分的学生为“数学尖子生”，得到如下数据表：请你根据已知条件完成下列2×2列联表，并判断是否有90%的把握认为“数学尖子生与性别有关”？

	数学尖子生	数学尖子生	合计
男生
女生
合计			100

参考数据：

P（K²≥k₂）	0.15	0.10	0.05	0.025	0.01	0.005
k₀	2.072	2.706	3.841	5.024	6.635	7.879

参考公式：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．

8．已知圆C：x²+y²-2x+a=0，设AB为圆C的一条直径，$\overrightarrow{OA}•\overrightarrow{OB}$=-6（O为坐标原点），则a的值为-6．

7．已知定义在（0，+∞）上的函数f（x）的导函数为f'（x），满足x²f'（x）+xf（x）=lnx，f（e）=$\frac{1}{e}$，则f（x）（　　）

	A．	有极大值，无极小值		B．	有极小值，无极大值
	C．	既有极大值又有极小值		D．	既无极大值也无极小值

0 239661 239669 239675 239679 239685 239687 239691 239697 239699 239705 239711 239715 239717 239721 239727 239729 239735 239739 239741 239745 239747 239751 239753 239755 239756 239757 239759 239760 239761 239763 239765 239769 239771 239775 239777 239781 239787 239789 239795 239799 239801 239805 239811 239817 239819 239825 239829 239831 239837 239841 239847 239855 266669