题目内容
8.已知圆C:x2+y2-2x+a=0,设AB为圆C的一条直径,$\overrightarrow{OA}•\overrightarrow{OB}$=-6(O为坐标原点),则a的值为-6.分析 设圆的半径为r,A(1+rcosα,rsinα),则B(1-rcosα,-rsinα),根据$\overrightarrow{OA}•\overrightarrow{OB}$=-6列方程解出r,再根据半径公式求出a.
解答 解:圆C的圆心为C(1,0),设圆C的半径为r,A(1+rcosα,rsinα),则B(1-rcosα,-rsinα),
∴$\overrightarrow{OA}•\overrightarrow{OB}$=1-r2cos2α-r2sin2α=1-r2=-6,
∴r=$\sqrt{7}$,
∴$\frac{\sqrt{4-4a}}{2}$=$\sqrt{7}$,解得a=-6.
故答案为:-6.
点评 本题考查了圆的一般方程,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.直线$\left\{\begin{array}{l}x=1+tcosα\\ y=-2+tsinα\end{array}$(t为参数,0≤a<π)必过点( )
| A. | (1,-2) | B. | (-1,2) | C. | (-2,1) | D. | (2,-1) |
16.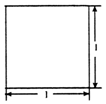 若一个底面是等腰直角三角形的直三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )
若一个底面是等腰直角三角形的直三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )
 若一个底面是等腰直角三角形的直三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )
若一个底面是等腰直角三角形的直三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )| A. | 6π或5π | B. | 3π或5π | C. | 6π | D. | 5π |
3.现要给一长、宽、高分别为3、2、1的长方体工艺品各面涂色,有红、橙、黄、蓝、绿五种颜色的涂料可供选择,要求相邻的面不能涂相同的颜色,且橙色跟黄色二选一,红色要涂两个面,则不同的涂色方案种数有( )
| A. | 48种 | B. | 72种 | C. | 96种 | D. | 108种 |
13.已知某条曲线的参数方程是$\left\{\begin{array}{l}x=2(t+\frac{1}{t})\\ y=2(t-\frac{1}{t})\end{array}$(t是参数),则该曲线是( )
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
20.已知在△ABC中,b2+a2-c2<0,且b>a,sinA+$\sqrt{2}$cosA=$\frac{5}{3}$,则tanA=( )
| A. | $\frac{2\sqrt{2}}{3}$或$\frac{4\sqrt{2}}{9}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{7\sqrt{2}}{8}$ | D. | $\frac{\sqrt{2}}{4}$或$\frac{7\sqrt{2}}{8}$ |
