题目内容
16.已知服从正态分布N(μ,σ2)的随机变量,在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ)和(μ-3σ,μ+3σ)内取值的概率分别为68.27%,95.45%和99.73%,某中学为10000名员工定制校服,设学生的身高(单位:cm)服从正态分布N(173,25),则适合身高在158~188cm范围内学生穿的校服大约要定制9973套.分析 判断均值和标准差,根据所给数据得出身高在158~188cm范围内学生人数.
解答 解:设学生身高为ξ,则ξ~N(173,25),
∴μ=173,σ=5,
∴P(158<ξ<188)=99.73%,
∴适合身高在158~188cm范围内学生穿的校服大约要定制10000×99.73%=9973套.
故答案为:9973.
点评 本题考查了正态分布的特点,属于中档题.

练习册系列答案
相关题目
4.在中学生综合素质评价某个维度的测评中,分“优秀”“合格”“尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并做出频数统计表如下:
表一:男生的测评结果
表二:女生的测评结果
(1)根据题意求表一和表二中的x和y的值;并由表中统计数据写下面的2×2列联表;
(2)根据所填的列联表判断是否有95%的把握认为“测评结果是否优秀与性别有关”.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
参考数据:
表一:男生的测评结果
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 非优秀 | |||
| 合计 |
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
参考数据:
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
11.观察数表:
根据数表中所反映的规律,第n+1行与第m列的交叉点上的数应该是m+n.
| 1 | 2 | 3 | 4 | …第一行 |
| 2 | 3 | 4 | 5 | …第二行 |
| 3 | 4 | 5 | 6 | …第三行 |
| 4 | 5 | 6 | 7 | …第四行 |
| 第一列 | 第二列 | 第三列 | 第四列 |
8.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )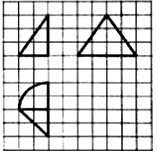

| A. | 2+π | B. | 2+4π | C. | 6+π | D. | 6+4π |
5.已知函数f(x)=6-x3,g(x)=ex-1,则这两个函数的导函数分别为( )
| A. | f′(x)=6-3x2,g′(x)=ex | B. | f′(x)=-3x2,g′(x)=ex-1 | ||
| C. | f′(x)=-3x2,g′(x)=ex | D. | f′(x)=6-3x2,g′(x)=ex-1 |