15.已知向量$\overrightarrow{m}$=(2cos2x,$\sqrt{3}$),$\overrightarrow{n}$=(1,sin2x),设函数$f(x)=\overrightarrow m•\overrightarrow n$,则下列关于函数y=f(x)的性质的描述正确的是( )
| A. | 关于直线$x=\frac{π}{12}$对称 | B. | 关于点$({\frac{5π}{12},0})$对称 | ||
| C. | 周期为2π | D. | y=f(x)在$({-\frac{π}{3},0})$上是增函数 |
14.若{an}是等差数列,且a1=-1,公差为-3,则a8等于( )
| A. | -7 | B. | -8 | C. | -22 | D. | 27 |
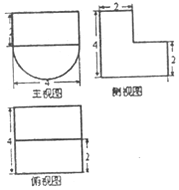
12. 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )
 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{4}{3}$ | B. | 8 | C. | 4 | D. | $\frac{8}{3}$ |
9.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入了部分数据,如下表:
(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数f(x)的解析式;
(2)令g(x)=f (x+$\frac{π}{3}$)-$\frac{1}{2}$,当x∈[-π,π]时,恒有不等式g(x)-a-3<0成立,求实数a的取值范围.
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{2π}{3}$ | $\frac{8π}{3}$ | |||
| Asin(ωx+φ) | 0 | 3 | 0 | -3 | 0 |
(2)令g(x)=f (x+$\frac{π}{3}$)-$\frac{1}{2}$,当x∈[-π,π]时,恒有不等式g(x)-a-3<0成立,求实数a的取值范围.
8.已知$\frac{π}{2}<A<π$,且sinA=$\frac{4}{5}$,那么sin2A等于( )
0 239427 239435 239441 239445 239451 239453 239457 239463 239465 239471 239477 239481 239483 239487 239493 239495 239501 239505 239507 239511 239513 239517 239519 239521 239522 239523 239525 239526 239527 239529 239531 239535 239537 239541 239543 239547 239553 239555 239561 239565 239567 239571 239577 239583 239585 239591 239595 239597 239603 239607 239613 239621 266669
| A. | $\frac{24}{25}$ | B. | $\frac{7}{25}$ | C. | $-\frac{12}{25}$ | D. | $-\frac{24}{25}$ |
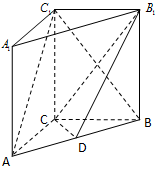 如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.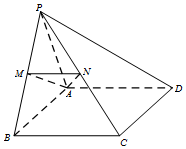 在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M、N分别为PB、PC的中点.
在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M、N分别为PB、PC的中点.