题目内容
10.已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与双曲线C2:x2-y2=4有相同的右焦点F2,点P是椭圆C1与双曲线C2在第一象限的公共点,若|PF2|=2,则椭圆C1的离心率等于$\frac{\sqrt{2}}{2}$.分析 利用双曲线、椭圆的定义,求出a,利用双曲线的性质,求出c,即可求出椭圆C1的离心率
解答 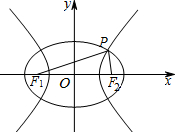 解:由题意,不妨设P在第一象限,
解:由题意,不妨设P在第一象限,
由双曲线C2:x2-y2=4的标准方程$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}=1$,则|PF1|-|PF2|=4,c=2$\sqrt{2}$
∵|PF2|=2,∴|PF1|=6,
∴2a=|PF2|+|PF2|=8,
∴a=4.
∵椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与双曲线C2:x2-y2=4有相同的右焦点F2,c=2$\sqrt{2}$,
∴椭圆C1的离心率为e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查椭圆与双曲线的几何性质,解题的关键是正确运用离心率的定义,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
18.将函数$y=4sin({4x+\frac{π}{6}})$的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将所得图象向右平移$\frac{π}{6}$个单位,则所得函数图象的一个对称中心为( )
| A. | (0,0) | B. | $({\frac{π}{3},0})$ | C. | $({\frac{π}{12},0})$ | D. | $({\frac{5}{8}π,0})$ |
15.已知向量$\overrightarrow{m}$=(2cos2x,$\sqrt{3}$),$\overrightarrow{n}$=(1,sin2x),设函数$f(x)=\overrightarrow m•\overrightarrow n$,则下列关于函数y=f(x)的性质的描述正确的是( )
| A. | 关于直线$x=\frac{π}{12}$对称 | B. | 关于点$({\frac{5π}{12},0})$对称 | ||
| C. | 周期为2π | D. | y=f(x)在$({-\frac{π}{3},0})$上是增函数 |
2.若不等式n2-n(λ+1)+7≥λ,对一切n∈N*恒成立,则实数λ的取值范围( )
| A. | λ≤3 | B. | λ≤4 | C. | 2≤λ≤3 | D. | 3≤λ≤4 |
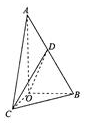 如图所示,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2$\sqrt{2}$,动点D在线段AB上.
如图所示,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2$\sqrt{2}$,动点D在线段AB上.