题目内容
9.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入了部分数据,如下表:| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{2π}{3}$ | $\frac{8π}{3}$ | |||
| Asin(ωx+φ) | 0 | 3 | 0 | -3 | 0 |
(2)令g(x)=f (x+$\frac{π}{3}$)-$\frac{1}{2}$,当x∈[-π,π]时,恒有不等式g(x)-a-3<0成立,求实数a的取值范围.
分析 (1)根据表中已知数据可得A,T,解得ω,φ的值,即可得解.
(2)由(1)可求g(x)=3$sin(\frac{1}{2}x+\frac{π}{3})$-$\frac{1}{2}$,由x∈[-π,π],解得-2≤g(x)≤$\frac{5}{2}$,由题意可得a+3>$\frac{5}{2}$,即可得解.
解答 解:(1)根据表中已知数据,解得$A=3,ω=\frac{1}{2},φ=\frac{π}{6}$.数据补全如下表:
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $-\frac{π}{3}$ | $\frac{2π}{3}$ | $\frac{5π}{3}$ | $\frac{8π}{3}$ | $\frac{11}{3}π$ |
| Asin(ωx+φ) | 0 | 3 | 0 | -3 | 0 |
函数表达式为$f(x)=3sin({\frac{1}{2}x+\frac{π}{6}})$…(5分)
(2)由(1)知$f(x)=3sin({\frac{1}{2}x+\frac{π}{6}})$,
∴g(x)=f (x+$\frac{π}{3}$)-$\frac{1}{2}$=3$sin[\frac{1}{2}(x+\frac{π}{3})+\frac{π}{6}]$-$\frac{1}{2}$=3$sin(\frac{1}{2}x+\frac{π}{3})$-$\frac{1}{2}$,…(7分)
∵x∈[-π,π]
∴($\frac{1}{2}$x+$\frac{π}{3}$)∈[-$\frac{π}{6}$,$\frac{5π}{6}$]…(8分)
∴-$\frac{1}{2}$≤$sin(\frac{1}{2}x+\frac{π}{3})$≤1,…(9分)
∴-2≤g(x)≤$\frac{5}{2}$,…(10分)
∵恒有不等式g(x)-a-3<0成立,
∴a+3>$\frac{5}{2}$,
∴a>-$\frac{1}{2}$,
∴a的取值范围是(-$\frac{1}{2}$,+∞).…(12分)
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,五点法作函数y=Asin(ωx+φ)的图象,正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
4.若y=sinxsin(x+$\frac{π}{3}$+φ)是一个奇函数,则φ可能的取值是( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
14.若{an}是等差数列,且a1=-1,公差为-3,则a8等于( )
| A. | -7 | B. | -8 | C. | -22 | D. | 27 |
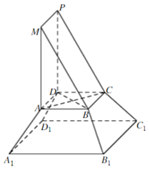 《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形,且侧棱与底面垂直的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABM-DCP与刍童的组合体中AB=AD,A1B1=A1D1.棱台体积公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分别为棱台上、下底面面积,h为棱台高.
《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形,且侧棱与底面垂直的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABM-DCP与刍童的组合体中AB=AD,A1B1=A1D1.棱台体积公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分别为棱台上、下底面面积,h为棱台高. 已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x-3.
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x-3.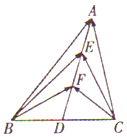 如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )