题目内容
13．某几何体的三视图如图所示，则该几何体的体积为16+8π．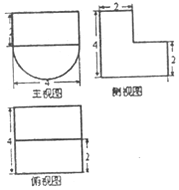
分析 判断几何体的形状，利用几何体的体积公式求解即可．
解答 
解：由三视图可知几何体是下部是半圆柱，上部是长方体，如图：几何体的体积为：2×2×4+$\frac{1}{2}×{2}^{2}×π×4$=16+8π．
故答案为：16+8π．
点评 本题考查三视图求解几何体的体积，判断几何体的形状是解题的关键，考查计算能力．
练习册系列答案
相关题目
3．函数f（x）是定义在（-∞，+∞）内的可导函数，且满足：xf'（x）+f（x）＞0，对于任意的正实数a，b，若a＞b，则必有（ ）
| A． | af（b）＞bf（a） | B． | bf（a）＞af（b） | C． | af（a）＜bf（b） | D． | af（a）＞bf（b） |
4．
甲、乙、丙．丁四辆玩具赛车同时从起点出发并做匀速直线运动，丙车最先到达终点．丁车最后到达终点．若甲、乙两车的s-t图象如图所示，则对于丙、丁两车的图象所在区域，判断正确的是（ ）
甲、乙、丙．丁四辆玩具赛车同时从起点出发并做匀速直线运动，丙车最先到达终点．丁车最后到达终点．若甲、乙两车的s-t图象如图所示，则对于丙、丁两车的图象所在区域，判断正确的是（ ）| A． | 丙在Ⅲ区域，丁在Ⅰ区域 | B． | 丙在Ⅰ区城，丁在Ⅲ区域 | ||
| C． | 丙在Ⅱ区域，丁在Ⅰ区域 | D． | 丙在Ⅲ区域，丁在Ⅱ区域 |
8．已知$\frac{π}{2}＜A＜π$，且sinA=$\frac{4}{5}$，那么sin2A等于（ ）
| A． | $\frac{24}{25}$ | B． | $\frac{7}{25}$ | C． | $-\frac{12}{25}$ | D． | $-\frac{24}{25}$ |
10．
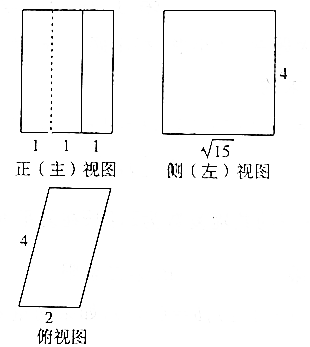如图，是一个几何体的正视图、侧视图、俯视图，且正视图、侧视图都是矩形，俯视图是平行四边形，则该几何体的体积是（ ）
如图，是一个几何体的正视图、侧视图、俯视图，且正视图、侧视图都是矩形，俯视图是平行四边形，则该几何体的体积是（ ）| A． | $\frac{8\sqrt{15}}{3}$ | B． | 8$\sqrt{15}$ | C． | $\frac{4\sqrt{15}}{3}$ | D． | 4$\sqrt{15}$ |