5．某学校课题组为了研究学生的数学成绩与学生细心程度的关系.在本校随机调查了100名学生进行研究．研究结果表明:在数学成绩及格的60名学生中有45人比较细心.另15人比较粗心,在数学成绩不及格的40名——青夏教育精英家教网——

5．某学校课题组为了研究学生的数学成绩与学生细心程度的关系，在本校随机调查了100名学生进行研究．研究结果表明：在数学成绩及格的60名学生中有45人比较细心，另15人比较粗心；在数学成绩不及格的40名学生中有10人比较细心，另30人比较粗心．
（1）试根据上述数据完成2×2列联表；

	数学成绩及格	数学成绩不及格	合计
比较细心	45	10	55
比较粗心	15	30	45
合计	60	40	100

（2）能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系．
参考数据：独立检验随机变量K²的临界值参考表：

P（K²≥k₀）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k₀	2.072	2.706	3.841	5.024	6.635	7.879	10.828

${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$（其中n=a+b+c+d）

4．在下列关于吸烟与患肺癌的2×2列联表中，d的值为（　　）

	不患肺癌	患肺癌	总计
不吸烟	7775	42	7817
吸烟		d
总计	9874		9965

3．以平面直角坐标系的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位．已知曲线C₁的参数方程为$\left\{\begin{array}{l}{x=cosα}\\{y=sinα}\end{array}\right.$，（α为参数，且α∈[0，π]），曲线C₂的极坐标方程为ρ=-2sinθ．
（Ⅰ）求C₁的极坐标方程与C₂的直角坐标方程；
（Ⅱ）若P是C₁上任意一点，过点P的直线l交C₂于点M，N，求|PM|•|PN|的取值范围．

2．已知复数z=x+（x-a）i，若对任意实数x∈（1，2），恒有|z|＞|z+i|，则实数a的取值范围为（　　）

$（{-∞，\frac{1}{2}}]$

$（{-∞，\frac{1}{2}}）$

$[\frac{5}{2}，+∞）$

$（{\frac{3}{2}，+∞}）$

1．（文）函数y=Asin（ωx+φ）（A＞0，ω＞0，$0≤φ≤\frac{π}{2}$）在x∈（0，9π）内只能取到一个最大值和一个最小值，且当x=π时，y有最大值4，当x=8π时，y有最小值-4．
（1）求出此函数的解析式以及它的单调递增区间；
（2）是否存在实数m，满足不等式$Asin（ω\sqrt{m+1}+φ）＞Asin（ω\sqrt{-m+4}+φ）$？若存在，求出m的取值范围；若不存在，请说明理由．

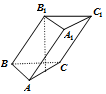已知一三棱柱ABC-A₁B₁C₁各棱长相等，B₁在底面ABC上的射影是AC的中点，则异面直线AA₁与BC所成角的余弦值为（　　）

$\frac{\sqrt{7}}{4}$

19．直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C₁的极坐标方程为$ρ=2\sqrt{2}sin（θ+\frac{π}{4}）$，直线l的参数方程为$\left\{{\begin{array}{l}{x=1-\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$（t为参数），直线l与曲线C₁交于A，B两点．
（Ⅰ）求|AB|的长度；
（Ⅱ）若曲线C₂的参数方程为$\left\{{\begin{array}{l}{x=3+\sqrt{2}cosα}\\{y=4+\sqrt{2}sinα}\end{array}}\right.$（α为参数），P为曲线C₂上的任意一点，求△PAB的面积的最小值．

18．直线y=kx+1与曲线y=x³+ax+b相切于点A（1，2），则b-a=5．

17．若m，n满足$\left\{\begin{array}{l}{m-n≥1}\\{m+n≤4}\\{m≥0}\\{n≥0}\end{array}\right.$，则u=m-2n的取值范围是$[{-\frac{1}{2}，4}]$．

16．已知在△ABC中，角A，B，C的对边分别为a，b，c，bsinA+acos（B+C）=0且$c=2，sinC=\frac{3}{5}$，
（1）求证：$B-A=\frac{π}{2}$；
（2）求a+b的值．

0 239404 239412 239418 239422 239428 239430 239434 239440 239442 239448 239454 239458 239460 239464 239470 239472 239478 239482 239484 239488 239490 239494 239496 239498 239499 239500 239502 239503 239504 239506 239508 239512 239514 239518 239520 239524 239530 239532 239538 239542 239544 239548 239554 239560 239562 239568 239572 239574 239580 239584 239590 239598 266669