题目内容
5．某学校课题组为了研究学生的数学成绩与学生细心程度的关系，在本校随机调查了100名学生进行研究．研究结果表明：在数学成绩及格的60名学生中有45人比较细心，另15人比较粗心；在数学成绩不及格的40名学生中有10人比较细心，另30人比较粗心．（1）试根据上述数据完成2×2列联表；
| 数学成绩及格 | 数学成绩不及格 | 合计 | |
| 比较细心 | 45 | 10 | 55 |
| 比较粗心 | 15 | 30 | 45 |
| 合计 | 60 | 40 | 100 |
参考数据：独立检验随机变量K2的临界值参考表：
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 （1）根据题意填写2×2列联表即可；
（2）根据2×2列联表求得K2的观测值，
对照临界值表即可得出结论．
解答 解：（1）填写2×2列联表如下；
| 数学成绩及格 | 数学成绩不及格 | 合计 | |
| 比较细心 | 45 | 10 | 55 |
| 比较粗心 | 15 | 30 | 45 |
| 合计 | 60 | 40 | 100 |
$k=\frac{{100×{{（{45×30-15×10}）}^2}}}{60×40×55×45}$=$\frac{2400}{99}＞24＞10.828$；
所以能在范错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系．
点评 本题考查了独立性检验的应用问题，是基础题．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
19．一家商场为了确定营销策略，进行了投入促销费用x和商场实际销售额y的试验，得到如下四组数据．
（1）求出x，y之间的回归直线方程$\widehaty$=$\widehatb$x+$\widehata$；
（2）若该商场计划营销额不低于600万元，则至少要投入多少万元的促销费用？
（注：$b=\frac{{\sum _{i=1}^n（{{x_i}-\bar x}）（{{y_i}-\bar y}）}}{{\sum _{i=1}^n{{（{{x_i}-\bar x}）}^2}}}=\frac{{\sum _{i=1}^n{x_i}{y_i}-n•\bar x•\bar y}}{{\sum _{i=1}^nx_i^2-n•{{\bar x}^2}}}，a=\bar y-b•\bar x$）
| 投入促销费用x（万元） | 2 | 3 | 5 | 6 |
| 商场实际营销额y（万元） | 100 | 200 | 300 | 400 |
（2）若该商场计划营销额不低于600万元，则至少要投入多少万元的促销费用？
（注：$b=\frac{{\sum _{i=1}^n（{{x_i}-\bar x}）（{{y_i}-\bar y}）}}{{\sum _{i=1}^n{{（{{x_i}-\bar x}）}^2}}}=\frac{{\sum _{i=1}^n{x_i}{y_i}-n•\bar x•\bar y}}{{\sum _{i=1}^nx_i^2-n•{{\bar x}^2}}}，a=\bar y-b•\bar x$）
20．
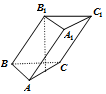已知一三棱柱ABC-A1B1C1各棱长相等，B1在底面ABC上的射影是AC的中点，则异面直线AA1与BC所成角的余弦值为（ ）
已知一三棱柱ABC-A1B1C1各棱长相等，B1在底面ABC上的射影是AC的中点，则异面直线AA1与BC所成角的余弦值为（ ）| A． | $\frac{\sqrt{7}}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{4}{3}$ |