题目内容

4．在下列关于吸烟与患肺癌的2×2列联表中，d的值为（　　）
不患肺癌患肺癌总计
不吸烟7775427817
吸烟d
总计98749965
A．48B．49C．50D．51

分析 根据列联表中各数据的关系，求出总计患肺癌的人数，
再计算吸烟且患肺癌的人数．

解答 解：在2×2列联表中，总计患肺癌的人数为9965-9874=91，
则吸烟且患肺癌的人数是d=91-42=49．
故选：B．

点评 本题考查了2×2列联表的应用问题，是基础题．

练习册系列答案
相关题目
18．给出如下五个结论：
①y=sinx在第一象限内是增函数；     
②存在区间（a，b），使y=cosx为减函数而sinx＜0；
③y=tanx在其定义域内为增函数；     
④y=cosx+sin（$\frac{π}{2}$-x）既有最大值和最小值，又是偶函数；
⑤y=sin|2x+$\frac{π}{6}$|的最小正周期为π．
其中正确结论的序号是④．
15．已知直线ax-by-2=0与曲线y=x2在点P（1，1）处的切线互相垂直，则$\frac{a}{b}$为（　　）
A．$\frac{2}{3}$B．-$\frac{2}{3}$C．$\frac{1}{2}$D．-$\frac{1}{2}$
12．已知甲、乙两个容器，甲容器容量为x，装满纯酒精，乙容器容量为z，其中装有体积为y的水（x，y＜z，单位：L）．现将甲容器中的液体倒入乙容器中，直至甲容器中液体倒完或乙容器盛满，搅拌使乙容器中两种液体充分混合，再将乙容器中的液体倒入甲容器中直至倒满，搅拌使甲容器中液体充分混合，如此称为一次操作，假设操作过程中溶液体积变化忽略不计．设经过n（n∈N*）次操作之后，乙容器中含有纯酒精an（单位：L），下列关于数，列{an}的说法正确的是（　　）
A．当x=y=a时，数列{an}有最大值$\frac{a}{2}$
B．设bn=an+1-an（n∈N*），则数列{bn}为递减数列
C．对任意的n∈N*，始终有${a_n}≤\frac{xy}{z}$
D．对任意的n∈N*，都有${a_n}≤\frac{xy}{x+y}$
19．直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为$ρ=2\sqrt{2}sin（θ+\frac{π}{4}）$，直线l的参数方程为$\left\{{\begin{array}{l}{x=1-\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$（t为参数），直线l与曲线C1交于A，B两点．
（Ⅰ）求|AB|的长度；
（Ⅱ）若曲线C2的参数方程为$\left\{{\begin{array}{l}{x=3+\sqrt{2}cosα}\\{y=4+\sqrt{2}sinα}\end{array}}\right.$（α为参数），P为曲线C2上的任意一点，求△PAB的面积的最小值．
9．某城市理论预测2000年到2004年人口总数与年份的关系如表所示
年份200x（年）01234
人口数y（十万）5781119
（1）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；
（2）此次估计2005年该城市人口总数．
（参考公式：用最小二乘法求线性回归方程系数的公式：$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$）
16．若数列{an}满足an-2an+1+an+2=0（n∈N*），且a1=2，a2=4，则数列{an}的通项公式为an=2n．
13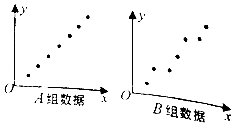．如图，给出了样本容量均为7的A、B两组样本数据的散点图，已知A组样本数据的相关系数为r1，B组数据的相关系数为r2，则（　　）
A．r1＞r2＞0B．r2＞r1＞0C．r1＜r2＜0D．r2＜r1＜0
14．在等差数列{an}中，a3=3，d=2，则a1=（　　）
A．1B．-1C．7D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网