15.已知直线ax-by-2=0与曲线y=x2在点P(1,1)处的切线互相垂直,则$\frac{a}{b}$为( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
14.某校高二2班学生每周用于数学学习的时间x(单位:h)与数学成绩y(单位:分)之间有如表数据:
(Ⅰ)求线性回归方程;
(Ⅱ)该班某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
参考数据:$\overline x=17.4$,$\overline y=74.9$,$\sum_{i=1}^{10}{{x_i}^2=3182}$,$\sum_{i=1}^{10}{{y_i}^2=58375}$,$\sum_{i=1}^{10}{{x_i}{y_i}=13578}$
回归直线方程参考公式:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
(Ⅱ)该班某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
参考数据:$\overline x=17.4$,$\overline y=74.9$,$\sum_{i=1}^{10}{{x_i}^2=3182}$,$\sum_{i=1}^{10}{{y_i}^2=58375}$,$\sum_{i=1}^{10}{{x_i}{y_i}=13578}$
回归直线方程参考公式:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.
7.已知i是虚数单位,则i+|i|在复平面上对应的点是( )
0 239401 239409 239415 239419 239425 239427 239431 239437 239439 239445 239451 239455 239457 239461 239467 239469 239475 239479 239481 239485 239487 239491 239493 239495 239496 239497 239499 239500 239501 239503 239505 239509 239511 239515 239517 239521 239527 239529 239535 239539 239541 239545 239551 239557 239559 239565 239569 239571 239577 239581 239587 239595 266669
| A. | (1,0) | B. | (0,1) | C. | (1,1) | D. | (1,-1) |
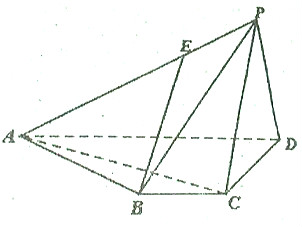 如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.
如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.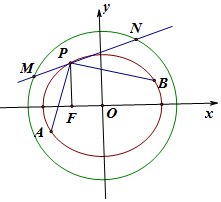 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),离心率为e,椭圆过点P(-2,3)与Q($\frac{2}{e}$,0).
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),离心率为e,椭圆过点P(-2,3)与Q($\frac{2}{e}$,0).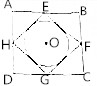 已知四边形ABCD中,E,F,G,H分别是线段AB,BC,CD,DA的中点,圆O为四边形EFGH的内切圆,则在正方形ABCD内投一点,该点落在圆O内的概率为$\frac{π}{8}$.
已知四边形ABCD中,E,F,G,H分别是线段AB,BC,CD,DA的中点,圆O为四边形EFGH的内切圆,则在正方形ABCD内投一点,该点落在圆O内的概率为$\frac{π}{8}$.