9．正项等比数列{an}中的a1.a4033是函数$f(x)=\frac{1}{3}{x^3}-4{x^2}+6x-3$的极值点.则log6a2017=( )A．1B．2C．$\frac{1}{2}$——青夏教育精英家教网——

9．正项等比数列{a_n}中的a₁，a₄₀₃₃是函数$f（x）=\frac{1}{3}{x^3}-4{x^2}+6x-3$的极值点，则log₆a₂₀₁₇=（　　）

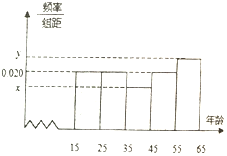某市文化部门为了了解本市市民对当地地方戏曲是否喜爱，从15-65岁的人群中随机抽样了n人，得到如下的统计表和频率分布直方图．

组号	分组	喜爱人数	喜爱人数占本组的频率
第1组	[15，25）	a	0.10
第2组	[25，35）	b	0.20
第3组	[35，45）	6	0.40
第4组	[45，55）	12	0.60
第5组	[55，65]	20	0.80

（1）写出其中a，b，n及x和y的值；
（2）若从第1，2，3，组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人，求这三组每组分别抽取多少人？
（3）在（2）抽取的6人中随机抽取2人，求抽取的2人年龄都在[35，45）的概率．

7．如图所示，矩形ABCD中，AB=3，BC=4，沿对角线BD把△ABD折起，使点A在平面BCD上的射影E落在BC上．

（1）求证：平面ACD⊥平面ABC；
（2）求三棱锥A-BCD的体积．

6．某工厂有A，B两种配件生产甲、乙两种产品，每生产一件甲产品使用4个A配件，耗时1h，每生产一件乙产品使用4个B配件，耗时2h，该厂每天最多可从配件厂获得24个A配件和16个B配件，每天生产总耗时不超过8h，若生产一件甲产品获利3万元，生产一件乙产品获利4万元，则通过恰当的生产安排，该工厂每天可获得的最大利润为22万元．

5．已知向量$\overrightarrow a，\overrightarrow b$满足$|\overrightarrow a|=2$，$|\overrightarrow b|=3$，$\overrightarrow a•\overrightarrow b=2$，则$|\overrightarrow a-\overrightarrow b|$=3．

4．已知i是虚数单位，若$z=\frac{a+i}{1+i}（a∈R）$为纯虚数，则a=（　　）

3．已知P=$\{0，1，\sqrt{2}\}$，Q={y|y=cosθ，θ∈R}，则P∩Q=（　　）

$\{0，1，\sqrt{2}\}$

2．已知S_n是等差数列{a_n}的前n项和，且s₆＞s₇＞s₅，给出下列五个命题：①d＞0；②S₁₁＞0；③S₁₂＜0；④数列{S_n}中的最大项为S₁₁；⑤|a₅|＞|a₇|．其中正确命题的个数为（　　）

1．已知全集U=R，集合A={x|y=lg（x-1）}，B={y|y=$\sqrt{{x}^{2}+2x+5}$}，则A∩（∁_UB）=（　　）

为了解某地高中生的身高情况，研究小组在该地高中生中随机抽出30名高中生的身高统计成如图所示的茎叶图（单位：cm）．
若身高在175cm以上（包括175cm）定义为“高个子”，身高在175cm以下（不包括175cm）定义为“非高个子”．
（1）求众数和平均数
（2）如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人，再从这5人中选2人，那么至少有1人是“高个子”的概率是多少？

0 239382 239390 239396 239400 239406 239408 239412 239418 239420 239426 239432 239436 239438 239442 239448 239450 239456 239460 239462 239466 239468 239472 239474 239476 239477 239478 239480 239481 239482 239484 239486 239490 239492 239496 239498 239502 239508 239510 239516 239520 239522 239526 239532 239538 239540 239546 239550 239552 239558 239562 239568 239576 266669