题目内容
3.已知P=$\{0,1,\sqrt{2}\}$,Q={y|y=cosθ,θ∈R},则P∩Q=( )| A. | ϕ | B. | {0} | C. | {0,1} | D. | $\{0,1,\sqrt{2}\}$ |
分析 根据集合的基本运算即可得到结论.
解答 解:Q={y|y=cos:θ,θ∈R}={y|-1≤y≤1},
则P∩Q={0,1},
故选:C.
点评 本题主要考查集合的基本运算,比较基础.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
8.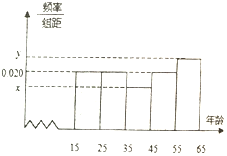 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
(1)写出其中a,b,n及x和y的值;
(2)若从第1,2,3,组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求抽取的2人年龄都在[35,45)的概率.
 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.| 组号 | 分组 | 喜爱人数 | 喜爱人数 占本组的频率 |
| 第1组 | [15,25) | a | 0.10 |
| 第2组 | [25,35) | b | 0.20 |
| 第3组 | [35,45) | 6 | 0.40 |
| 第4组 | [45,55) | 12 | 0.60 |
| 第5组 | [55,65] | 20 | 0.80 |
(2)若从第1,2,3,组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求抽取的2人年龄都在[35,45)的概率.
15.已知集合A={-1,0,1},B={x|0≤x≤1},则A∩(∁RB)=( )
| A. | -1 | B. | {-1} | C. | {1} | D. | {-1,1} |
13.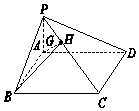 如图,H为四棱锥P-ABCD的棱PC的三等分点,且PH=$\frac{1}{2}$HC,点G在AH上,AG=mAH.四边形ABCD为平行四边形,若G,B,P,D四点共面,则实数m等于( )
如图,H为四棱锥P-ABCD的棱PC的三等分点,且PH=$\frac{1}{2}$HC,点G在AH上,AG=mAH.四边形ABCD为平行四边形,若G,B,P,D四点共面,则实数m等于( )
 如图,H为四棱锥P-ABCD的棱PC的三等分点,且PH=$\frac{1}{2}$HC,点G在AH上,AG=mAH.四边形ABCD为平行四边形,若G,B,P,D四点共面,则实数m等于( )
如图,H为四棱锥P-ABCD的棱PC的三等分点,且PH=$\frac{1}{2}$HC,点G在AH上,AG=mAH.四边形ABCD为平行四边形,若G,B,P,D四点共面,则实数m等于( )| A. | $\frac{1}{4}$ | B. | $\frac{4}{3}$P,D | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
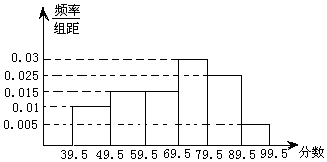 如图,从参加环保知识竞赛的学生中抽出80名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出80名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题: