题目内容
7.如图所示,矩形ABCD中,AB=3,BC=4,沿对角线BD把△ABD折起,使点A在平面BCD上的射影E落在BC上.
(1)求证:平面ACD⊥平面ABC;
(2)求三棱锥A-BCD的体积.
分析 (1)由AE⊥平面BCD得AE⊥CD,结合CD⊥BC得出CD⊥平面ABC,故而平面ACD⊥平面ABC;
(2)证明AB⊥平面ACD,故而VA-BCD=VB-ACD=$\frac{1}{3}$•S△ACD•AB.
解答 (1)证明:∵AE⊥平面BCD,CD?平面BCD,
∴AE⊥CD.
又BC⊥CD,且AE∩BC=E,
∴CD⊥平面ABC.
又CD?平面ACD,
∴平面ACD⊥平面ABC.
(2)由(1)知,CD⊥平面ABC,又AB?平面ABC,
∴CD⊥AB.
又∵AB⊥AD,CD∩AD=D,
∴AB⊥平面ACD.
∴VA-BCD=VB-ACD=$\frac{1}{3}$•S△ACD•AB.
又∵在△ACD中,AC⊥CD,AD=BC=4,AB=CD=3,
∴AC=$\sqrt{A{D^2}-C{D^2}}=\sqrt{{4^2}-{3^2}}=\sqrt{7}$.
∴VA-BCD=$\frac{1}{3}×\frac{1}{2}×\sqrt{7}×3×3=\frac{{3\sqrt{7}}}{2}$.
点评 本题考查了面面垂直的判定,线面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
17.下列函数是偶函数的是( )
| A. | y=tan3x | B. | y=cos2x+1 | C. | y=2sinx-1 | D. | y=2x |
15.设a=log32,b=ln2,$c={5^{\frac{1}{2}}}$则( )
| A. | c>b>a | B. | a>b>c | C. | a>c>b | D. | b>a>c |
2.已知Sn是等差数列{an}的前n项和,且s6>s7>s5,给出下列五个命题:①d>0;②S11>0;③S12<0;④数列{Sn}中的最大项为S11;⑤|a5|>|a7|.其中正确命题的个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司M的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.
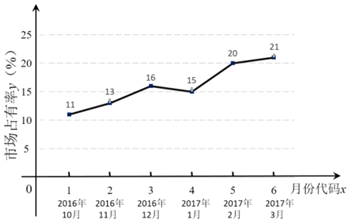
(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系.求y关于x的线性回归方程,并预测M公司2017年4月份的市场占有率;
(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
经测算,平均每辆单车每年可以带来收入500元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率.如果你是M公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
参考数据:,$\sum_{i=1}^6{({x_i}-\overline x)({y_i}}-\overline y)=35$,$\sum_{i=1}^6{{{({x_i}-\overline x)}^2}}$=17.5.
参考公式:
回归直线方程为$\hat y=\hat bx+\hat a$其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{t}$.

(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系.求y关于x的线性回归方程,并预测M公司2017年4月份的市场占有率;
(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
报废年限 车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
| A | 20 | 35 | 35 | 10 | 100 |
| B | 10 | 30 | 40 | 20 | 100 |
参考数据:,$\sum_{i=1}^6{({x_i}-\overline x)({y_i}}-\overline y)=35$,$\sum_{i=1}^6{{{({x_i}-\overline x)}^2}}$=17.5.
参考公式:
回归直线方程为$\hat y=\hat bx+\hat a$其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{t}$.
17.已知函数f(x)是偶函数,当0<x1<x2时,[f(x2)-f(x1)](x2-x1)>0恒成立,设$a=f(-\frac{1}{2}),b=f(2),c=f(3)$,则a,b,c的大小关系为( )
| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<b<a |
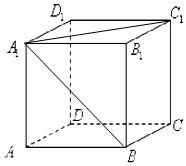 如图,正方体ABCD-A1B1C1D1棱长为1.
如图,正方体ABCD-A1B1C1D1棱长为1.