题目内容
1．已知全集U=R，集合A={x|y=lg（x-1）}，B={y|y=$\sqrt{{x}^{2}+2x+5}$}，则A∩（∁UB）=（ ）| A． | [1，2] | B． | [1，2） | C． | （1，2] | D． | （1，2） |
分析 根据题意，由集合的表示方法分析A、B，求出B的补集，由集合的交集定义计算可得答案．
解答 解：集合A={x|y=lg（x-1）}，为函数y=lg（x-1）的定义域，
则A={x|y=lg（x-1）}=（1，+∞），
B={y|y=$\sqrt{{x}^{2}+2x+5}$}=[2，+∞），
∁UB=（-∞，2）
A∩（∁UB）=（1，2）；
故选：D．
点评 本题考查集合交并补的混合运算，关键是掌握集合的表示方法．
练习册系列答案
口算能手系列答案
相关题目
11．设f（x）是定义在R上周期为2的奇函数，当0≤x≤1时，f（x）=x2-x，则$f（{-\frac{5}{2}}）$=（ ）
| A． | $-\frac{1}{4}$ | B． | $-\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
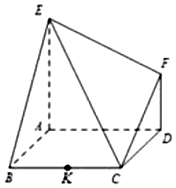如图，已知多面体EABCDF的底面ABCD是边长为2的正方形，EA⊥底面ABCD，FD∥EA，且$FD=\frac{1}{2}EA=1$．
10．随机变量X～N（1，4），若p（x≥2）=0.2，则p（0≤x≤1）为（ ）
| A． | 0.2 | B． | 0.6 | C． | 0.4 | D． | 0.3 |