13.已知点A(2,-3),B(-3,-2),直线m过P(1,1),且与线段AB相交,求直线m的斜率k的取值范围为( )
| A. | $k≥\frac{3}{4}或k≤-4$ | B. | $k≥\frac{3}{4}或k≤-\frac{1}{4}$ | C. | -4≤k≤$\frac{3}{4}$ | D. | $\frac{3}{4}$≤k≤4 |
12.已知二面角α-AB-β的平面角是锐角θ,α内一点C到β的距离为3,点C到棱AB的距离为4,那么cosθ的值等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{{3\sqrt{7}}}{7}$ | D. | $\frac{\sqrt{7}}{4}$ |
11.设l、m是两条不同的直线,α是一个平面,则下列说法正确的是( )
| A. | 若l⊥m,m⊆α则l⊥α | B. | 若l∥α,m⊆α则l∥m | C. | 若l⊥α,l∥m则m⊥α | D. | 若l∥α,m∥α则l∥m |
9.某校高二年级共有2000人,其中男生1100人,女生900人,为调查该年级学生每周平均体育运动时间的情况,采用分成抽样的方法抽取200人进行分析,统计的数据如表(时间单位:小时).
男、女运动时间情况的调查表:
(Ⅰ)计算x,y的值,根据以上统计数据完成下面的每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该级部学生的每周平均体育运动时间与性别有关”.
附:
(Ⅱ)在每周平均体育运动时间在8小时以上的被调查的人中,喜欢乒乓球的有6人,其中男生4人,女生2人;级部决定从这4名男省中选2人,2名女生中选1人,组成代表队参加校运动会,则男生A和女生E恰好都被选中的概率是多少?
0 239333 239341 239347 239351 239357 239359 239363 239369 239371 239377 239383 239387 239389 239393 239399 239401 239407 239411 239413 239417 239419 239423 239425 239427 239428 239429 239431 239432 239433 239435 239437 239441 239443 239447 239449 239453 239459 239461 239467 239471 239473 239477 239483 239489 239491 239497 239501 239503 239509 239513 239519 239527 266669
男、女运动时间情况的调查表:
| 时间 | (0,2) | [2,4) | [4,6) | [6,8) | 8小时以上 |
| 男生人数 | 10 | 25 | 35 | 30 | x |
| 女生人数 | 15 | 30 | 25 | y | 5 |
| 男生 | 女生 | 总计 | |
| 平均时间不超过6小时 | |||
| 平均时间超过6小时 | |||
| 总计 |
| K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ | P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 6.635 | 7.789 |
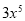 +
+ -8x+5在x=2时的值。
-8x+5在x=2时的值。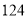 人,其中女性
人,其中女性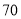 人,男性
人,男性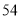 人.女性中有
人.女性中有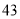 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有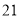 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动.
人主要的休闲方式是运动.