题目内容
11.设l、m是两条不同的直线,α是一个平面,则下列说法正确的是( )| A. | 若l⊥m,m⊆α则l⊥α | B. | 若l∥α,m⊆α则l∥m | C. | 若l⊥α,l∥m则m⊥α | D. | 若l∥α,m∥α则l∥m |
分析 在A中,l与α相交、平行或l?α;在B中,l与m平行或异面;在C中,由线面垂直的判定定理得m⊥α;在D中,l与m相交、平行或异面.
解答 解:由l、m是两条不同的直线,α是一个平面,知:
在A中,若l⊥m,m⊆α,则l与α相交、平行或l?α,故A错误;
在B中,若l∥α,m⊆α,则l与m平行或异面,故B错误;
在C中,若l⊥α,l∥m,则由线面垂直的判定定理得m⊥α,故C正确;
在D中,若l∥α,m∥α,则l与m相交、平行或异面,故D错误.
故选:C.
点评 本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、空间想象能力、运算求解能力,考查函数与方程思想、化归与转化思想、数形结合思想,是中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
1.将函数f(x)=ax+1(a>0,a≠1)的图象向右平移2个单位得到函数g(x)的图象,则( )
| A. | 存在实数x0,使得g(x0)=1 | B. | 当x1<x2时,必有g(x1)<g(x2) | ||
| C. | g(2)的取值与实数a有关 | D. | 函数g(f(x))的图象必过定点 |
2.直线l1:Ax+By+C1=0关于直线l2:Ax+By+C2=0(C1≠C2)对称的直线方程是( )
| A. | Ax+By+(C1-2C2)=0 | B. | Ax+By+(C2-2C1)=0 | C. | Ax+By+(2C2-C1)=0 | D. | Ax+By+(2C1-C2)=0 |
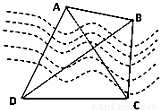
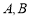 两点都在河的对岸(不可到达),为了测量
两点都在河的对岸(不可到达),为了测量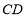 ,测得:
,测得: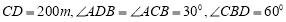 ,则
,则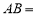 ()
()
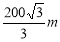 B.
B.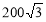
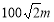 D.数据不够,无法计算
D.数据不够,无法计算