题目内容
10.在平面直角坐标系中,曲线C的参数方程为:$\left\{\begin{array}{l}x=\sqrt{5}cosθ\\ y=3+\sqrt{5}sinθ\end{array}\right.$(其中θ为参数).(Ⅰ) 以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求曲线C的极坐标方程;
( II)直线l的参数方程为:$\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.$(其中t为参数),直线l与曲线C分别交于A,B两点,且$|AB|=2\sqrt{3}$,求直线l的斜率.
分析 (Ⅰ)先把曲线C的参数方程化为直角坐标方程,由此能求出曲线C的极坐标方程.
(Ⅱ)求出直线l的直角坐标方程为y=tanα•x,圆心C(0,3)到直线的距离d=$\frac{|3|}{\sqrt{1+ta{n}^{2}α}}$,再由$|AB|=2\sqrt{3}$,利用勾股定理求出tan2α=$\frac{7}{2}$,由此能求出直线l的斜率.
解答 解:(Ⅰ)∵曲线C的参数方程为:$\left\{\begin{array}{l}x=\sqrt{5}cosθ\\ y=3+\sqrt{5}sinθ\end{array}\right.$(其中θ为参数),
∴曲线C的直角坐标方程为x2+(y-3)2=5,即x2+y2-6y+4=0,
∴曲线C的极坐标方程为ρ2-6ρsinθ+4=0.
(Ⅱ)∵直线l的参数方程为:$\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.$(其中t为参数),
∴直线l的直角坐标方程为y=tanα•x,
圆心C(0,3)到直线的距离d=$\frac{|3|}{\sqrt{1+ta{n}^{2}α}}$,
∵直线l与曲线C分别交于A,B两点,且$|AB|=2\sqrt{3}$,
∴$\sqrt{{r}^{2}-{d}^{2}}=\frac{|AB|}{2}$,
即$\sqrt{5-\frac{9}{1+ta{n}^{2}α}}$=$\sqrt{3}$,解得tan2α=$\frac{7}{2}$,
∴tanα=±$\frac{\sqrt{14}}{2}$.
∴直线l的斜率为$±\frac{\sqrt{14}}{2}$.
点评 本题考查圆、直线方程、极坐标方程、直角坐标方程、参数方程、点到直线距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 18 | B. | 24 | C. | 30 | D. | 32 |
| A. | A(x-x0)+B(y-y0)=0 | B. | B(x-x0)+A(y-y0)=0 | C. | A(x-x0)-B(y-y0)=0 | D. | B(x-x0)-A(y-y0)=0 |
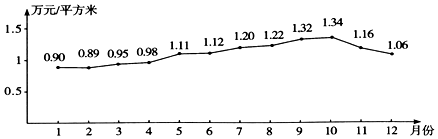
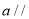 平面
平面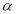 ,直线
,直线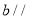 平面
平面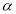 ,则直线
,则直线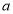 不一定平行于直线
不一定平行于直线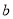
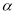 不垂直于平面
不垂直于平面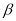 ,则
,则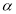 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面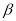
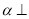 平面
平面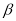 ,则
,则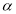 内一定不存在直线平行于平面
内一定不存在直线平行于平面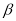
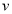 ,平面
,平面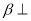 平面
平面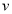 ,
,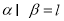 ,则
,则 一定垂直于平面
一定垂直于平面