题目内容
7.已知函数f(x)=blnx+a(a>0,b>0)在x=1处的切线与圆(x-2)2+y2=4相交于A、B两点,并且弦长|AB|=2$\sqrt{3}$,则$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$-$\frac{{a}^{2}}{{b}^{2}}$的最小值为5.
分析 利用导数求出f(x)在x=1处的切线方程,
根据圆心到直线的距离d、弦长以及半径的关系,得出a、b的关系,
再代入$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$-$\frac{{a}^{2}}{{b}^{2}}$中,利用基本不等式求出它的最小值.
解答 解:f(x)=blnx+a(a>0,b>0),
∴f′(x)=$\frac{b}{x}$,
∴切线l的斜率为k=f′(1)=b,且f(1)=a;
∴f(x)在x=1处的切线l的方程为y-a=b(x-1),
即bx-y+a-b=0;
又切线l与圆(x-2)2+y2=4交于A、B两点,且弦长|AB|=2$\sqrt{3}$,
∴圆心(2,0)到切线l的距离为d=$\frac{|2b+a-b|}{\sqrt{{b}^{2}+1}}$,
由d2+${(\frac{|AB|}{2})}^{2}$=r2,
∴$\frac{{(a+b)}^{2}}{{b}^{2}+1}$+${(\sqrt{3})}^{2}$=22,
化简得2ab+a2=1,
∴$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$-$\frac{{a}^{2}}{{b}^{2}}$=$\frac{2ab{+a}^{2}}{{a}^{2}}$+$\frac{2ab{+a}^{2}}{{b}^{2}}$-$\frac{{a}^{2}}{{b}^{2}}$
=$\frac{2b}{a}$+1+$\frac{2a}{b}$
=2($\frac{b}{a}$+$\frac{a}{b}$)+1≥2•2$\sqrt{\frac{b}{a}•\frac{a}{b}}$+1=4+1=5,
当且仅当a=b时取“=”;
∴所求的最小值为5.
故答案为:5.
点评 本题考查了利用导数求出函数的切线方程,以及点到直线的距离、弦长以及半径的关系,和用基本不等式求出最值的应用问题,是综合题.

| A. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)min=0 | B. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)min=-1 | C. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)max=$\frac{3}{4}$ | D. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)max=$\frac{2}{3}$ |
 ,如果不等式
,如果不等式 的解集是
的解集是 则不等式
则不等式 的解集是___________
的解集是___________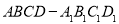 中,
中, 在线段
在线段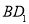 上,且
上,且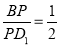 ,
,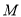 为线段
为线段 上的动点,则三棱锥
上的动点,则三棱锥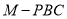 的体积为( )
的体积为( )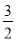
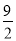 D.与
D.与 点的位置有关
点的位置有关