15.命题p:将函数y=cosx•sinx的图象向右平移$\frac{3π}{4}$个单位可得到y=$\frac{1}{2}$cos2x的图象;命题q:对?m>0,双曲线2x2-y2=m2的离心率为$\sqrt{3}$,则下列结论正确的是( )
| A. | p是假命题 | B. | ¬p是真命题 | C. | p∨q是真命题 | D. | p∧q是假命题 |
13.定义运算$|\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}|$=ad-bc,复数z满足$|\begin{array}{l}{z}&{1}\\{i}&{i}\end{array}|$=2+i,则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.已知公差为d的等差数列{an}前n项和为Sn,若有确定正整数n0,对任意正整数m,${S}_{{n}_{0}}$•${S}_{{n}_{0}+m}$<0恒成立,则下列说法错误的是( )
| A. | a1•d<0 | B. | |Sn|有最小值 | ||
| C. | ${a}_{{n}_{0}}$•${a}_{{n}_{0}+1}$>0 | D. | ${a}_{{n}_{0}+1}•{a}_{{n}_{0}+2}$>0 |
9.为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如表:
某校研究性学习小组,从汽车市场上随机选取了M辆纯电动乘用车,根据其续驶里程R(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(1)求x、y、z、M的值;
(2)若从这M辆纯电动乘用车任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为X(单位:万元),求X的分布列和数学期望值E(X).
0 239268 239276 239282 239286 239292 239294 239298 239304 239306 239312 239318 239322 239324 239328 239334 239336 239342 239346 239348 239352 239354 239358 239360 239362 239363 239364 239366 239367 239368 239370 239372 239376 239378 239382 239384 239388 239394 239396 239402 239406 239408 239412 239418 239424 239426 239432 239436 239438 239444 239448 239454 239462 266669
| 新能源汽车补贴标准 | |||
| 车辆类型 | 续驶里程R(公里) | ||
| 100≤R<180 | 180≤R<280 | <280 | |
| 纯电动乘用车 | 2.5万元/辆 | 4万元/辆 | 6万元/辆 |
| 分组 | 频数 | 频率 |
| 100≤R<180 | 3 | 0.3 |
| 180≤R<280 | 6 | x |
| R≥280 | y | z |
| 合计 | M | 1 |
(2)若从这M辆纯电动乘用车任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为X(单位:万元),求X的分布列和数学期望值E(X).
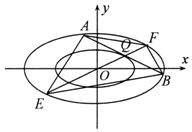 在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.
在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.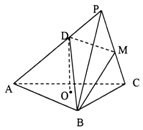 如图,三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.
如图,三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.