题目内容
11.已知公差为d的等差数列{an}前n项和为Sn,若有确定正整数n0,对任意正整数m,${S}_{{n}_{0}}$•${S}_{{n}_{0}+m}$<0恒成立,则下列说法错误的是( )| A. | a1•d<0 | B. | |Sn|有最小值 | ||
| C. | ${a}_{{n}_{0}}$•${a}_{{n}_{0}+1}$>0 | D. | ${a}_{{n}_{0}+1}•{a}_{{n}_{0}+2}$>0 |
分析 利用已知及其等差数列的单调性通项公式与求和公式即可得出.
解答 解:∵公差为d的等差数列{an},有确定正整数n0,对任意正整数m,${S}_{{n}_{0}}$•${S}_{{n}_{0}+m}$<0恒成立,
∴a1与d异号,即a1•d<0,|Sn|有最小值,${a}_{{n}_{0}}$•${a}_{{n}_{0}+1}$<0,${a}_{{n}_{0}+2}$•${a}_{{n}_{0}+1}$>0.
因此C不正确.
故选:C.
点评 本题考查了等差数列的单调性通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
6.函数y=2x+1-2x2的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
3.变量x,y满足线性约束条件$\left\{\begin{array}{l}{3x+y-2≤0}\\{y-x≤2}\\{y≥-x-1}\end{array}\right.$,目标函数z=kx+y仅在点(0,2)取得最大值,则k的取值范围是( )
| A. | -3<k<1 | B. | k>1 | C. | -1<k<1 | D. | -1<k<3 |
20.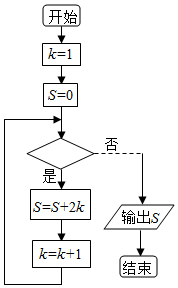 如果执行如图的程序框图,输出的S=30,则判断框处为( )
如果执行如图的程序框图,输出的S=30,则判断框处为( )
 如果执行如图的程序框图,输出的S=30,则判断框处为( )
如果执行如图的程序框图,输出的S=30,则判断框处为( )| A. | k<5 | B. | k≤5 | C. | k≥6 | D. | k>6 |
1.已知集合A={x|x2-2x<0},B={x|y=log2(x-1)},则A∪B=( )
| A. | (0,+∞) | B. | (1,2) | C. | (2,+∞) | D. | (-∞,0) |