题目内容
12.过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点F(1,0)的直线与椭圆C交于两点A、B,自A、B向直线x=5作垂线,垂足分别为A1、B1,且$\frac{|A{A}_{1}|}{AF}$=$\sqrt{5}$.(1)求椭圆C的方程;
(2)记△AFA1、△FA1B1、△BFB1的面积分别为S1、S2、S3,证明:$\frac{{S}_{1}•{S}_{3}}{{{S}_{2}}^{2}}$是定值,并求出该定值.
分析 (1)设点A(x,y),写出|AA1|、|AF|的表达式,由$\frac{|A{A}_{1}|}{AF}$=$\sqrt{5}$求出椭圆C的方程;
(2)根据题意可设直线方程为x=my+1,A(x1,y1),B(x2,y2);由$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1}\end{array}\right.$得(4m2+5)y2+8my-16=0,由根与系数的关系,结合题意求出△AFA1的面积S1,△FA1B1的面积S2,△BFB1的面积S3,计算$\frac{{S}_{1}{•S}_{3}}{{{S}_{2}}^{2}}$的值即可.
解答 解:(1)设点A(x,y),则|AA1|=5-x,|AF|=$\sqrt{{(x-1)}^{2}{+y}^{2}}$,
由$\frac{|A{A}_{1}|}{AF}$=$\sqrt{5}$,得$\frac{|5-x|}{\sqrt{{(x-1)}^{2}{+y}^{2}}}$=$\sqrt{5}$,
化简得$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1,
由A是椭圆C上任一点,
∴椭圆C的方程为$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1;
(2)证明:∵直线AB的斜率不可以为0,而可以不存在,
∴可设直线方程为:x=my+1;
设A(x1,y1),B(x2,y2);
由$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,
消去x得(4m2+5)y2+8my-16=0;
∴$\left\{\begin{array}{l}{{y}_{1}{+y}_{2}=-\frac{8m}{{4m}^{2}+5}}\\{{{y}_{1}y}_{2}=-\frac{16}{{4m}^{2}+5}}\end{array}\right.$(*);
由题意:△AFA1的面积为S1=$\frac{1}{2}$|AA1|•|y1|=$\frac{1}{2}$|5-x1|•|y1|,
△FA1B1的面积为S2=$\frac{1}{2}$|BB1|•|y2|=$\frac{1}{2}$|5-x2|•|y2|,
△BFB1的面积为S3=$\frac{1}{2}$|A1B1|•4=2|y1-y2|;
∴$\frac{{S}_{1}{•S}_{3}}{{{S}_{2}}^{2}}$=$\frac{1}{16}$•$\frac{(5{-x}_{1})(5{-x}_{2})({{-y}_{1}y}_{2})}{{{(y}_{1}{-y}_{2})}^{2}}$
=$\frac{1}{16}$•$\frac{(4-{my}_{1})(4-{my}_{2})({{-y}_{1}y}_{2})}{{{(y}_{1}{-y}_{2})}^{2}}$
=-$\frac{1}{16}$•$\frac{{{y}_{1}y}_{2}[16-4m{(y}_{1}{+y}_{2}){{{+m}^{2}y}_{1}y}_{2}]}{{{(y}_{1}{+y}_{2})}^{2}-{{4y}_{1}y}_{2}}$,
将(*)式代入上述式子,化简并计算可得
$\frac{{S}_{1}{•S}_{3}}{{{S}_{2}}^{2}}$=-$\frac{1}{16}$•$\frac{-\frac{16}{{4m}^{2}+5}•[16-4m•(-\frac{8m}{{4m}^{2}+5}){+m}^{2}•(-\frac{16}{{4m}^{2}+5})]}{{(-\frac{8m}{{4m}^{2}+5})}^{2}-4•(-\frac{16}{{4m}^{2}+5})}$=$\frac{1}{4}$;
∴$\frac{{S}_{1}•{S}_{3}}{{{S}_{2}}^{2}}$是定值,且该定值是$\frac{1}{4}$.
(注意直线AB的点斜式方程需讨论斜率不存在的情况,没有讨论须扣分)
点评 本题考查了直线与椭圆方程的应用问题,也考查了椭圆的标准方程与直线的斜率存在与否进行分类讨论的问题,是综合题.

 特高级教师点拨系列答案
特高级教师点拨系列答案| A. | {x|x<-3} | B. | {x|-3<x<2} | C. | {x|x<2} | D. | {x|-3≤x<2} |
| A. | $\frac{\sqrt{41}}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
($\sqrt{2}$+1),试用以上给出的公式求得△ABC的面积为( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{5}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
| A. | $\frac{13}{10}$ | B. | $\frac{19}{10}$ | C. | $\frac{3}{2}$ | D. | -2 |
| A. | $-\frac{1}{5}-\frac{3}{5}i$ | B. | $\frac{1}{5}+\frac{3}{5}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $\frac{1}{5}-\frac{3}{5}i$ |
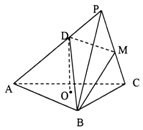 如图,三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.
如图,三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.