题目内容
13.定义运算$|\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}|$=ad-bc,复数z满足$|\begin{array}{l}{z}&{1}\\{i}&{i}\end{array}|$=2+i,则复数z在复平面内对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由新定义列式,变形后利用复数代数形式的乘除运算化简求出z的坐标得答案.
解答 解:由$|\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}|$=ad-bc,
得$|\begin{array}{l}{z}&{1}\\{i}&{i}\end{array}|$=iz-i=2+i,
∴iz=2+2i,则z=$\frac{2+2i}{i}=\frac{(2+2i)(-i)}{-{i}^{2}}=2-2i$,
∴复数z在复平面内对应的点的坐标为(2,-2),位于第四象限.
故选:D.
点评 本题考查复数的代数表示法及其几何意义,考查复数代数形式的乘除运算,是基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
3.若$\overline z$是z的共轭复数,且满足$\overline z({1-i})$=3+i,则z=( )
| A. | 1+2i | B. | -1+2i | C. | 1-2i | D. | -1-2i |
8.已知f(x)=$\left\{\begin{array}{l}{-2{x}^{2}+3x,-2≤x<0}\\{ln\frac{1}{x+1},0≤x≤2}\end{array}\right.$,若g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,则实数a的取值范围为( )
| A. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | B. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | C. | (0,$\frac{1}{e}$) | D. | (0,$\frac{1}{2e}$) |
5.△ABC中,角A、B、C的对边分别为a、b、c,G是平面△ABC上一点,且满足a•$\overrightarrow{GA}$+b•$\overrightarrow{GB}$+c•$\overrightarrow{GC}$=0,则G是△ABC中的( )
| A. | 内心 | B. | 外心 | C. | 重心 | D. | 垂心 |
3.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一条渐近线方程为2x+y=0,则C的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
 一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮?
一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮?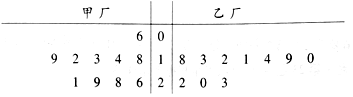 某种产品的产量以其质量指标值(单位:克)衡量,质量指标值越大表明质量越好,且质量指标值大于17时,该产品为优等品,现在为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取10件样品,测量样品的质量指标值,得到如图所示的茎叶图.
某种产品的产量以其质量指标值(单位:克)衡量,质量指标值越大表明质量越好,且质量指标值大于17时,该产品为优等品,现在为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取10件样品,测量样品的质量指标值,得到如图所示的茎叶图.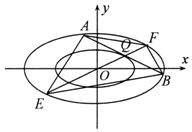 在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.
在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.