18.如图所示,在△ABC内随机选取一点P,则△PBC的面积不超过△ABC面积一半的概率是( )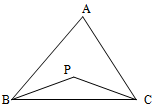

| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
17.已知单位向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a+3\overrightarrow b}|=\sqrt{13}$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
14.设{an}是公差不为0的等差数列,满足a42+a52=a62+a72,则{an}的前10项和S10=( )
| A. | -10 | B. | -5 | C. | 0 | D. | 5 |
13.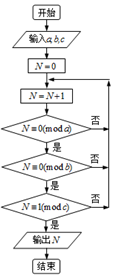 若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡4(bmod6),如图程序框图的算法源于我国古代《孙子算经》中的“孙子定理”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )
若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡4(bmod6),如图程序框图的算法源于我国古代《孙子算经》中的“孙子定理”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )
 若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡4(bmod6),如图程序框图的算法源于我国古代《孙子算经》中的“孙子定理”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )
若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡4(bmod6),如图程序框图的算法源于我国古代《孙子算经》中的“孙子定理”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )| A. | 6 | B. | 9 | C. | 12 | D. | 21 |
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左,右焦点分别为F1,F2,双曲线上一点P满足PF2⊥x轴.若|F1F2|=12,|PF2|=5,则该双曲线的离心率为( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{12}{5}$ | D. | $\frac{13}{12}$ |
10.执行如图所示的程序框图,如果输出的结果为0,那么输入的x为( )


| A. | $\frac{1}{9}$ | B. | -1或1 | C. | 1 | D. | -1 |
9.执行所给的程序框图,则输出的值是( )

0 239254 239262 239268 239272 239278 239280 239284 239290 239292 239298 239304 239308 239310 239314 239320 239322 239328 239332 239334 239338 239340 239344 239346 239348 239349 239350 239352 239353 239354 239356 239358 239362 239364 239368 239370 239374 239380 239382 239388 239392 239394 239398 239404 239410 239412 239418 239422 239424 239430 239434 239440 239448 266669

| A. | $\frac{1}{55}$ | B. | $\frac{1}{58}$ | C. | $\frac{1}{61}$ | D. | $\frac{1}{64}$ |
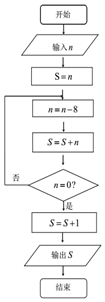 《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.
《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.