10.某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲,乙,丙三地实施人工降雨,其实验统计结果如下
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲,乙,丙三地中缓解旱情的个数”为随机变量X,求X的分布列和数学期望.
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
| A | 甲 | 2次 | 6次 | 4次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲,乙,丙三地中缓解旱情的个数”为随机变量X,求X的分布列和数学期望.
5.通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下2×2列联表:
(Ⅰ)从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
(Ⅱ)根据以上2×2列联表,是否有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 男生 | 女生 | 合计 | |
| 挑同桌 | 30 | 40 | 70 |
| 不挑同桌 | 20 | 10 | 30 |
| 总计 | 50 | 50 | 100 |
(Ⅱ)根据以上2×2列联表,是否有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
3.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
0 239245 239253 239259 239263 239269 239271 239275 239281 239283 239289 239295 239299 239301 239305 239311 239313 239319 239323 239325 239329 239331 239335 239337 239339 239340 239341 239343 239344 239345 239347 239349 239353 239355 239359 239361 239365 239371 239373 239379 239383 239385 239389 239395 239401 239403 239409 239413 239415 239421 239425 239431 239439 266669
| A. | y=lgx | B. | y=cosx | C. | y=|x| | D. | y=sinx |
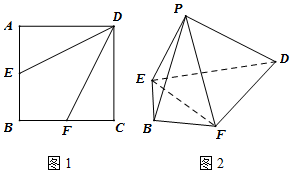 如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.
如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.