题目内容
3.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )| A. | y=lgx | B. | y=cosx | C. | y=|x| | D. | y=sinx |
分析 根据题意,依次分析选项中函数的奇偶性以及在(0,+∞)单调性,综合即可得答案.
解答 解:根据题意,依次分析选项:
对于A、y=lgx为对数函数,不是偶函数,故A不符合题意,
对于B、y=cosx,为偶函数,但在(0,+∞)上不具有单调性,不符合题意,
对于C、y=|x|=$\left\{\begin{array}{l}{x,x≥0}\\{-x,x<0}\end{array}\right.$,为偶函数,在(0,+∞)上,f(x)=x为增函数,符合题意,
对于D、y=sinx,为正弦函数,为奇函数,不符合题意,
故选:C.
点评 本题考查函数奇偶性、单调性的判定,关键是掌握常见函数的奇偶性、单调性.

练习册系列答案
相关题目
11.设集合A={x|x2-1<0},B={x|y=ln(x-1)},则A∪B=( )
| A. | (-1,1) | B. | (-1,+∞) | C. | (-1,1)∪(1,+∞) | D. | (1,+∞) |
15.已知f(x)=alnx-x2在区间(0,1)内任取两个不相等的实数p、q,不等式$\frac{f(p)-f(q)}{p-q}>1$恒成立,则实数a的取值范围为( )
| A. | (3,5) | B. | (-∞,0) | C. | (3,5] | D. | [3,+∞) |
11.$\int{\begin{array}{l}{\frac{π}{4}}\\ 0\end{array}}({sinx-acosx})dx=-\frac{{\sqrt{2}}}{2}$,则实数a等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | -1 | D. | $-\sqrt{3}$ |
 已知AB,CD是圆O两条相互垂直的直径,弦DE交AB的延长线于点F,若DE=24,EF=18,求OE的长.
已知AB,CD是圆O两条相互垂直的直径,弦DE交AB的延长线于点F,若DE=24,EF=18,求OE的长.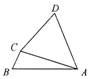 如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.
如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.