题目内容
6.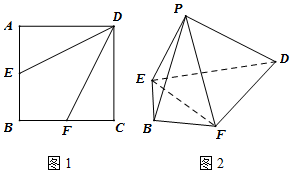 如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.
如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.(Ⅰ)求证:DP⊥EF;
(Ⅱ)求四棱锥P-BFDE的体积.
分析 (Ⅰ)推导出PD⊥PE,PD⊥PF,从而PD⊥平面PEF,由此能证明PD⊥EF.
(Ⅱ)推导出PE=PF=BE=BF=2,EF=$\sqrt{4+4}=2\sqrt{2}$,BD=$\sqrt{16+16}=4\sqrt{2}$,从而S四边形BFDE=$\frac{1}{2}×BD×EF$=8,P到平面BFDE的距离d=$\sqrt{P{F}^{2}-(\frac{EF}{2})^{2}}$=$\sqrt{2}$,由此能求出四棱锥P-BFDE的体积.
解答 证明:(Ⅰ)∵边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,
将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P,
∴PD⊥PE,PD⊥PF,
∵PE∩PF=P,∴PD⊥平面PEF,
∵EF?平面PEF,∴PD⊥EF.
解:(Ⅱ)∵边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,
将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P,
∴PE=PF=BE=BF=2,EF=$\sqrt{4+4}=2\sqrt{2}$,BD=$\sqrt{16+16}=4\sqrt{2}$,
∴S四边形BFDE=$\frac{1}{2}×BD×EF$=$\frac{1}{2}×4\sqrt{2}×2\sqrt{2}$=8,
P到平面BFDE的距离d=$\sqrt{P{F}^{2}-(\frac{EF}{2})^{2}}$=$\sqrt{4-2}$=$\sqrt{2}$,
∴四棱锥P-BFDE的体积:
$V=\frac{1}{3}×{S}_{四边形BFDE}×d$=$\frac{1}{3}×8×\sqrt{2}$=$\frac{8\sqrt{2}}{3}$.
点评 本题线线垂直的证明,考查几何体的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 190 | B. | 114 | C. | 60 | D. | 120 |
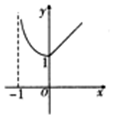
| A. | f(x)=eln|x+1| | B. | f(x)=eln|x-1| | C. | f(x)=e|ln(x+1)| | D. | f(x)=e|ln(x-1)| |
| A. | $-5\sqrt{2}$ | B. | $-3\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 0 |
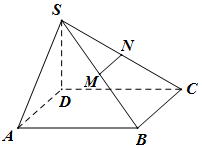 已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC中点,过MN作平面MNPQ分别与线段CD,AB相交于点P,Q.
已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC中点,过MN作平面MNPQ分别与线段CD,AB相交于点P,Q.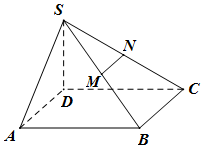 已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.
已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.