10.已知实数x,y满足$\left\{\begin{array}{l}{2x-y-2≥0}\\{x+y-1≤0}\\{y+1≥0}\end{array}\right.$,z=mx+y的最大值为3,则实数m的值是( )
| A. | -2 | B. | 3 | C. | 8 | D. | 2 |
9.若从集合{1,2,3,4,5}中随机地选出三个元素,则满足其中两个元素的和等于第三个元素的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
8.已知a=21.3,b=40.7,c=ln6,则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
7.设全集U=R,A={x|x2-x-6≥0},B={x|x>1},则(∁UA)∪B=( )
| A. | {x|x≥-2} | B. | {x|x>-2} | C. | {x|1<x<3} | D. | {x|1<x≤3} |
3.某印刷厂为了研究印刷单册书籍的成本y(单位:元)与印刷册数x(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表.
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到了两个回归方程,方程甲:$\widehat{y}$(1)=$\frac{4}{x}$+1.1,方程乙:$\widehat{y}$(2)=$\frac{6.4}{{x}^{2}}$+1.6.
(Ⅰ)为了评价两种模型的拟合效果,完成以下任务.
(i)完成下表(计算结果精确到0.1);
(ii)分别计算模型甲与模型乙的残差平方和Q1和Q2,并通过比较Q1,Q2的大小,判断哪个模型拟合效果更好.
(Ⅱ)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为10千册,若印刷厂以每册5元的价格将书籍出售给订货商,试估计印刷厂二次印刷获得的利润.(按(Ⅰ)中拟合效果较好的模型计算印刷单册书的成本)
0 239235 239243 239249 239253 239259 239261 239265 239271 239273 239279 239285 239289 239291 239295 239301 239303 239309 239313 239315 239319 239321 239325 239327 239329 239330 239331 239333 239334 239335 239337 239339 239343 239345 239349 239351 239355 239361 239363 239369 239373 239375 239379 239385 239391 239393 239399 239403 239405 239411 239415 239421 239429 266669
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
(Ⅰ)为了评价两种模型的拟合效果,完成以下任务.
(i)完成下表(计算结果精确到0.1);
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 | |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值$\widehat{{y}_{i}}$(1) | 2.4 | 2.1 | 1.6 | ||
| 残值$\widehat{{e}_{i}}$(1) | 0 | -0.1 | 0.1 | |||
模型乙 | 估计值$\widehat{{y}_{i}}$(2) | 2.3 | 2 | 1.9 | ||
| 残值$\widehat{{e}_{i}}$(2) | 0.1 | 0 | 0 | |||
(Ⅱ)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为10千册,若印刷厂以每册5元的价格将书籍出售给订货商,试估计印刷厂二次印刷获得的利润.(按(Ⅰ)中拟合效果较好的模型计算印刷单册书的成本)
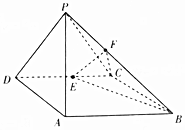 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.