题目内容
10.已知实数x,y满足$\left\{\begin{array}{l}{2x-y-2≥0}\\{x+y-1≤0}\\{y+1≥0}\end{array}\right.$,z=mx+y的最大值为3,则实数m的值是( )| A. | -2 | B. | 3 | C. | 8 | D. | 2 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,分类讨论得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答  解:由实数x,y满足$\left\{\begin{array}{l}{2x-y-2≥0}\\{x+y-1≤0}\\{y+1≥0}\end{array}\right.$作出可行域如图,
解:由实数x,y满足$\left\{\begin{array}{l}{2x-y-2≥0}\\{x+y-1≤0}\\{y+1≥0}\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{2x-y-2=0}\\{y+1=0}\end{array}\right.$,解得A($\frac{1}{2}$,-1),
联立$\left\{\begin{array}{l}{2x-y-2=0}\\{x+y-2=0}\end{array}\right.$,解得B(1,0),同理C(2,-1)
化目标函数z=mx+y为y=-mx+z,
当直线z=mx+y经过C点时,取得最大值3;∴3=2m-1,解得m=2.
故选:D.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,考查分类讨论的数学思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知函数f(x)=(x-b)lnx+x2在区间[1,e]上单调递增,则实数b的取值范围是( )
| A. | (-∞,-3] | B. | (-∞,2e] | C. | (-∞,3] | D. | (-∞,2e2+2e] |
18.定义:$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,如$|\begin{array}{l}{1}&{2}\\{3}&{4}\end{array}|$=1×4-2×3=-2.当x∈R时,$|\begin{array}{l}{{e}^{x}}&{3}\\{1}&{2}\end{array}|$≥k恒成立,则实数k的取值范围是( )
| A. | (-∞,-3] | B. | (-∞,-3) | C. | (-3,+∞) | D. | [-3,+∞) |
19.已知集合A={x|$lo{g}_{\frac{1}{2}}$(x-1)>1},B={x|x2-2x-3>0},则“x∈A”是“x∈B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.某学校食堂在高一年级学生中抽查了100名学生进行饮食习惯调查,结果如表:
(I)从这100人中随机抽取1人,求抽到喜欢吃辣的学生概率;
(II)试判断有多大把握认为喜欢吃辣与性别有关;
(III)已知在被调查的学生中有5人来自一班,其中有2人喜欢吃辣,从这5人中随机抽取3人,求其中恰有1人喜欢吃辣的概率.
下面临界值表仅供参考:
$({参考公式:{K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}},其中n=a+b+c+d})$.
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 30 | 10 | 40 |
| 女生 | 25 | 35 | 60 |
| 合计 | 55 | 45 | 100 |
(II)试判断有多大把握认为喜欢吃辣与性别有关;
(III)已知在被调查的学生中有5人来自一班,其中有2人喜欢吃辣,从这5人中随机抽取3人,求其中恰有1人喜欢吃辣的概率.
下面临界值表仅供参考:
| P(K2≥k0) | 0.15 | 100. | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 8411. | 5.024 | 6.635 | 7.879 | 10.828 |
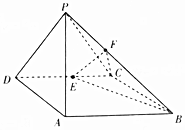 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.