题目内容
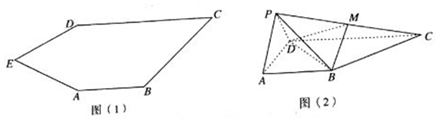
4.如图(1),五边形ABCDE中,ED=EA,AB∥CD,CD=2AB,∠EDC=150°.如图(2),将△EAD沿AD折到△PAD的位置,得到四棱锥P-ABCD.点M为线段PC的中点,且BM⊥平面PCD.
(Ⅰ)求证:平面PAD⊥平面ABCD;
(Ⅱ)若四棱锥P-ABCD的体积为2$\sqrt{3}$,求四面体BCDM的体积.
分析 (Ⅰ)取PD的中点N,连结AN、MN,推导出四边形ABMN是平行四边形,从而AN∥BM,推导出AN⊥平面PCD,从而AN⊥PD,AN⊥CD,再求出CD⊥AD,从而CD⊥平面PAD,由此能证明平面PAD⊥平面ABCD.
(Ⅱ)设四棱锥P-ABCD的高为h,四边形ABCD的面积为S,由${S}_{△BCD}=\frac{2}{3}S$,四面体BCDM的底面BCD上的高为$\frac{h}{2}$,能求出四面体BCDM的体积.
解答 证明:(Ⅰ)取PD的中点N,连结AN、MN,
则MN∥CD,且MN=$\frac{1}{2}$CD,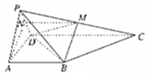
又AB∥CD,AB=$\frac{1}{2}$CD,
∴MN∥AB,MN=AB,
∴四边形ABMN是平行四边形,
∴AN∥BM,
又BM⊥面PCD,∴AN⊥平面PCD,
∴AN⊥PD,AN⊥CD,
由ED=EA,即PD=PA,及N为PD的中点,
得△PAD为等边三角形,∴∠PDA=60°,
又∠EDC=150°,∴∠CDA=90°,
∴CD⊥AD,∴CD⊥平面PAD,
又∵CD?平面ABCD,
∴平面PAD⊥平面ABCD.
解:(Ⅱ)设四棱锥P-ABCD的高为h,四边形ABCD的面积为S,
则${V}_{P-ABCD}=\frac{1}{3}hs=2\sqrt{3}$,
又${S}_{△BCD}=\frac{2}{3}S$,四面体BCDM的底面BCD上的高为$\frac{h}{2}$,
∴四面体BCDM的体积:
VBCDM=$\frac{1}{3}×\frac{h}{2}×{S}_{△BCD}$=$\frac{1}{6}×\frac{2}{3}sh$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查面面垂直的证明,考查几何体的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、是中档题.

| A. | {x|-2<x<1} | B. | {x|x<-2} | C. | {x|x<1} | D. | {x|x<2} |
| A. | [0,2) | B. | [0,2] | C. | [-1,$\frac{1}{2}$] | D. | [0,+∞) |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
 某农科所发现,一中作物的年收获量y(单位:kg)与它”相近“作物的株数x具有线性相关关系(所谓两株作物”相近“是指它们的直线距离不超过1m),并分别记录了相近作物的株数为1,2,3,5,6,7时,该作物的年收获量的相关数据如下:
某农科所发现,一中作物的年收获量y(单位:kg)与它”相近“作物的株数x具有线性相关关系(所谓两株作物”相近“是指它们的直线距离不超过1m),并分别记录了相近作物的株数为1,2,3,5,6,7时,该作物的年收获量的相关数据如下:| X | 1 | 2 | 3 | 5 | 6 | 7 |
| y | 60 | 55 | 53 | 46 | 45 | 41 |
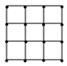
(Ⅱ)农科所在如图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,其中每一个小正方形的面积为1,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收获量以线性回归方程计算所得数据为依据)
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线y=a+bx的斜率和截距的最小二乘估计分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
 已知AB,CD是圆O两条相互垂直的直径,弦DE交AB的延长线于点F,若DE=24,EF=18,求OE的长.
已知AB,CD是圆O两条相互垂直的直径,弦DE交AB的延长线于点F,若DE=24,EF=18,求OE的长.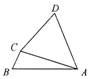 如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.
如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.