题目内容
7．设全集U=R，A={x|x2-x-6≥0}，B={x|x＞1}，则（∁UA）∪B=（ ）| A． | {x|x≥-2} | B． | {x|x＞-2} | C． | {x|1＜x＜3} | D． | {x|1＜x≤3} |
分析 解不等式得集合A，根据补集与并集的定义写出（∁UA）∪B．
解答 解：全集U=R，A={x|x2-x-6≥0}={x|x≤-2或x≥3}，
B={x|x＞1}，
∴∁UA={x|-2＜x＜3}，
∴（∁UA）∪B={x|x＞-2}．
故选：B．
点评 本题考查了解不等式与补集和并集的运算问题，是基础题．
练习册系列答案
相关题目
17．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的右焦点为F，以双曲线C的实轴为直径的圆Ω与双曲线的渐近线在第一象限交于点P，若kFP=-$\frac{b}{a}$，则双曲线C的渐近线方程为（ ）
| A． | y=±x | B． | y=±2x | C． | y=±3x | D． | y=±4x |
18．“|x-1|+|x+2|≤5”是“-3≤x≤2”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
12．
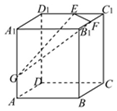如图所示，在正方体ABCD-A1B1C1D1中，点G在棱AA1上，AG=$\frac{1}{3}$AA1，E，F分别是棱
C1D1，B1C1的中点，过E，F，G三点的截面α将正方体分成两部分，则正方体的四个侧面被截面α截得的上、下两部分面积之比为（ ）
如图所示，在正方体ABCD-A1B1C1D1中，点G在棱AA1上，AG=$\frac{1}{3}$AA1，E，F分别是棱C1D1，B1C1的中点，过E，F，G三点的截面α将正方体分成两部分，则正方体的四个侧面被截面α截得的上、下两部分面积之比为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
19．已知函数f（x）=$\left\{{\begin{array}{l}{f（{x+2}），x＜3}\\{{{（{\frac{1}{2}}）}^x}，x≥3}\end{array}}$，则f（-4）=（ ）
| A． | $\frac{1}{16}$ | B． | $\frac{1}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
16．已知数列{an}，若点（n，an）（n∈N*）在经过点（10，6）的定直线上，则数列{an}的前19项和S19的值为（ ）
| A． | 190 | B． | 114 | C． | 60 | D． | 120 |