19.如果x,y满足$\left\{\begin{array}{l}{x-2y-4≤0}\\{x+y-1≥0}\\{2x-y-2≥0}\end{array}\right.$,则z=$\frac{y+1}{x+1}$的取值范围是( )
| A. | [0,2) | B. | [0,2] | C. | [-1,$\frac{1}{2}$] | D. | [0,+∞) |
18.定义:$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,如$|\begin{array}{l}{1}&{2}\\{3}&{4}\end{array}|$=1×4-2×3=-2.当x∈R时,$|\begin{array}{l}{{e}^{x}}&{3}\\{1}&{2}\end{array}|$≥k恒成立,则实数k的取值范围是( )
| A. | (-∞,-3] | B. | (-∞,-3) | C. | (-3,+∞) | D. | [-3,+∞) |
17.已知曲线y=x3在点(1,1)处的切线与直线ax+y+1=0垂直,则a的值是( )
| A. | -1 | B. | 1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
16.已知复数z1=$\frac{m-i}{i}$(m∈R)与z2=2i的虚部相等,则复数z1对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.某校高二文科100名学生参加了语数英学科竞赛,年级为了解这些学生语文和数学成绩的情况,将100名学生的语文和数学成绩统计如表:
(I)若数学成绩的优秀率为35%,现利用随机抽样从数学成绩“优秀”的学生中抽取1名学生,求该生语文成绩为“及格”的概率;
(II)在语文成绩为“良”的学生中,已知m≥10,n≥10,求数学成绩“优”比“良”的人数少的概率.
0 239234 239242 239248 239252 239258 239260 239264 239270 239272 239278 239284 239288 239290 239294 239300 239302 239308 239312 239314 239318 239320 239324 239326 239328 239329 239330 239332 239333 239334 239336 239338 239342 239344 239348 239350 239354 239360 239362 239368 239372 239374 239378 239384 239390 239392 239398 239402 239404 239410 239414 239420 239428 266669
| 语文 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 13 | m | 5 |
| 良 | 12 | n | 9 | |
| 及格 | 10 | 14 | 7 | |
(II)在语文成绩为“良”的学生中,已知m≥10,n≥10,求数学成绩“优”比“良”的人数少的概率.
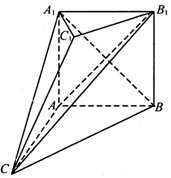 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.