题目内容
20.抛物线C:y2=2px(p>0)的焦点为F,E是C的准线上位于x轴上方的一点,直线EF与C在第一象限交于点M,在第四象限交于点N,且|EM|=2|MF|=2,则点N到y轴的距离为$\frac{9}{4}$.分析 由题意可知丨FM丨=1,|EM|=2,丨EF丨=3,根据相似三角形的性质,即可求得p的值,由丨EN丨=2丨DN丨,根据抛物线的定义,即可求得丨DN丨=3,点N到y轴的距离为丨DN丨-$\frac{p}{2}$.
解答 解:过M,N做MH⊥l,ND⊥l,垂足分别为H,D,
由抛物线的定义可得丨FM丨=丨MH丨,丨FN丨=丨DN丨
|EM|=2|MF|=2,则丨FM丨=1,|EM|=2,丨EF丨=3,
∴∠EMH=$\frac{π}{3}$,∠MEH=$\frac{π}{6}$,
∴p=$\frac{3}{2}$,抛物线的标准方程为y2=3x,
在Rt△EDN中,sin∠MED=$\frac{丨DN丨}{丨EN丨}$,
则丨EN丨=2丨DN丨,即丨EM丨+丨MF丨+丨DN丨=2丨DN丨,
则丨DN丨=3,
点N到y轴的距离为丨DN丨-$\frac{p}{2}$=3-$\frac{3}{4}$=$\frac{9}{4}$,
故答案为:$\frac{9}{4}$.
点评 本题考查抛物线的简单几何性质,抛物线的定义,考查三角形的相似,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
10.已知函数f(x)=$\left\{{\begin{array}{l}{lnx,x>0}\\{\frac{m}{x},x<0}\end{array}}$,若f(x)-f(-x)=0有四个不同的根,则m的取值范围是( )
| A. | (0,2e) | B. | (0,e) | C. | (0,1) | D. | (0,$\frac{1}{e}$) |
8.下列说法正确的是( )
| A. | 已知命题p,q,若p∨(¬q)为真命题,则q一定是假命题 | |
| B. | 命题“?x∈R,2x>0”的否定是“$?{x_0}∈R,{2^{x_0}}<0$” | |
| C. | “$x=\frac{π}{4}$”是“tan x=l”的充分不必要条件 | |
| D. | “若x1>1,x2>1,则x1+x2>2”的否命题是真命题 |
12.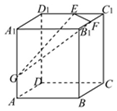 如图所示,在正方体ABCD-A1B1C1D1中,点G在棱AA1上,AG=$\frac{1}{3}$AA1,E,F分别是棱
如图所示,在正方体ABCD-A1B1C1D1中,点G在棱AA1上,AG=$\frac{1}{3}$AA1,E,F分别是棱
C1D1,B1C1的中点,过E,F,G三点的截面α将正方体分成两部分,则正方体的四个侧面被截面α截得的上、下两部分面积之比为( )
 如图所示,在正方体ABCD-A1B1C1D1中,点G在棱AA1上,AG=$\frac{1}{3}$AA1,E,F分别是棱
如图所示,在正方体ABCD-A1B1C1D1中,点G在棱AA1上,AG=$\frac{1}{3}$AA1,E,F分别是棱C1D1,B1C1的中点,过E,F,G三点的截面α将正方体分成两部分,则正方体的四个侧面被截面α截得的上、下两部分面积之比为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
9. 如图,在四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC=$\frac{π}{2}$.
如图,在四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC=$\frac{π}{2}$.
(1)求证:B1C1∥平面BCD1;
(2)求证:平面A1ABB1⊥平面BCD1.
 如图,在四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC=$\frac{π}{2}$.
如图,在四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC=$\frac{π}{2}$.(1)求证:B1C1∥平面BCD1;
(2)求证:平面A1ABB1⊥平面BCD1.
10.设函数f(x)=$\left\{\begin{array}{l}{2x+1,x≤0}\\{{e}^{x},x>0}\end{array}\right.$,则满足f(f(m))>f(m)+1的m的取值范围是( )
| A. | $({-\frac{1}{2},+∞})$ | B. | )(0,+∞) | C. | (-1,+∞) | D. | .$({-\frac{1}{3},+∞})$ |
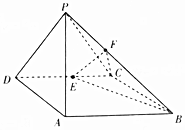 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.