题目内容
14.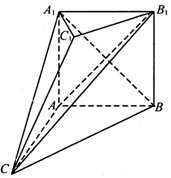 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.(I)求证:A1B⊥B1C;
(II)求证:AB1∥平面A1C1C.
分析 (I)欲证明A1B⊥B1C,只需推知A1B⊥平面AB1C;
(Ⅱ)取BC的中点E,证明四边形CEB1C1为平行四边形,可得B1E∥C1C,从而可得B1E∥面A1C1C,再证明AE∥面A1C1C,利用面面平行的判定,可得面B1AE∥面A1C1C,从而可得AB1∥面A1C1C.
解答  解:(I)证明:设A1B与AB1交于点O,连接CO.
解:(I)证明:设A1B与AB1交于点O,连接CO.
四边形ABB1A1是正方形,
∴A1B⊥AB1,A1O=BO,
∴在△A1BC中,A1C=BC,∴A1B⊥CO.
又因为A1B∩CO=O,∴A1B⊥面AB1C,
又B1C?面AB1C,A1B⊥B1C;
(Ⅱ)取BC中点D,连接AD,C1D,BB1D.
∵$\left\{\begin{array}{l}{{B}_{1}{C}_{1}∥BC,{B}_{1}C{1}_{1}=\frac{1}{2}BC}\\{{B}_{1}{C}_{1}∥DC,{B}_{1}{C}_{1}∥BD}\end{array}\right.$∴四边形B1C1CD是平行四边形.
∴B1D∥CC1,B1B∥C1D,又B1B∥A1A,B1B=A1A,∴A1A∥C1D,A1A=C1D,
∴四边形A1ADC1是平行四边形.∴AD∥A1C1.
又B1D?面A1C1C,AD?面A1C1C,∴B1D∥面A1C1C,AD∥面A1C1C,
又B1D∩AD=D,∴平面.AB1D∥面A1C1C,
∵AB1?面AB1D,∴AB1∥平面A1C1C.
点评 本题考查面面垂直,考查线面平行,解题的关键是掌握面面垂直的判定方法,正确运用面面平行判断线面平行,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.函数$f(x)={e^x}+\frac{1}{x}$(x>0),若x0满足f'(x0)=0,设m∈(0,x0),n∈(x0,+∞),则( )
| A. | f'(m)<0,f'(n)<0 | B. | f'(m)>0,f'(n)>0 | C. | f'(m)<0,f'(n)>0 | D. | f'(m)>0,f'(n)<0 |
5.设变量x,y满足约束条件$\left\{\begin{array}{l}x+y≥2\\ x-y≤2\\ 3y≥2\end{array}\right.$,则x2+y2的最小值为( )
| A. | $\frac{5}{3}$ | B. | $\frac{7}{3}$ | C. | $\frac{20}{9}$ | D. | 2 |
9.已知由一组样本数据确定的回归直线方程为$\hat y=1.5x+1$,且$\overline x=2$,发现有两组数据(2.6,2.8)与(1.4,5.2)误差较大,去掉这两组数据后,重新求得回归直线的斜率为1.4,那么当x=6时,$\hat y$的估计值为( )
| A. | 9.6 | B. | 10 | C. | 10.6 | D. | 9.4 |
19.如果x,y满足$\left\{\begin{array}{l}{x-2y-4≤0}\\{x+y-1≥0}\\{2x-y-2≥0}\end{array}\right.$,则z=$\frac{y+1}{x+1}$的取值范围是( )
| A. | [0,2) | B. | [0,2] | C. | [-1,$\frac{1}{2}$] | D. | [0,+∞) |
4.若复数z满足iz=l+3i,其中i为虚数单位,则$\overline z$=( )
| A. | -3+i | B. | -3-i | C. | 3+i | D. | 3-i |
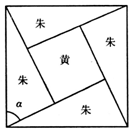 三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为$\frac{π}{3}$,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为1-$\frac{\sqrt{3}}{2}$.
三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为$\frac{π}{3}$,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为1-$\frac{\sqrt{3}}{2}$.