19．雾霾天气对城市环境造成很大影响，按照国家环保部发布的标准：居民区的PM2.5（大气中直径小于或等于2.5微米的颗粒物）年平均浓度不得超过35微克/立方米．某市环保部门加强了对空气质量的监测，抽取某居民区监测点的20天PM2.5的24小时平均浓度的监测数据，制成茎叶图如图1：
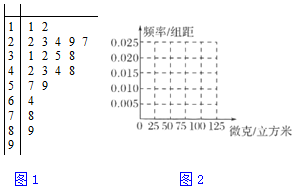
（Ⅰ）完成如下频率分布表，并在所给的坐标系中画出（0，100）的频率分布直方图如图2；
（Ⅱ）从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中，随机抽取2天，求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率．
（Ⅰ）完成如下频率分布表，并在所给的坐标系中画出（0，100）的频率分布直方图如图2；
| 组别 | PM2.5浓度（微粒、立方米） | 频数（天） | 频率 |
| 第一组 | （0，25] | 5 | 0.25 |
| 第二组 | （25，50] | 10 | 0.5 |
| 第三组 | （50，75] | 3 | 0.15 |
| 第四组 | （75，100] | 2 | 0.1 |
17．某早餐店每天制作甲、乙两种口味的糕点共n（n∈N*）份，每份糕点的成本1元，售价2元，如果当天卖不完，剩下的糕点作废品处理，该早餐店发现这两种糕点每天都有剩余，为此整理了过往100天这两种糕点的日销量（单位：份），得到如下统计数据：
以这100天记录的各销量的频率作为各销量的概率，假设这两种糕点的日销量相互独立．
（1）记该店这两种糕点每日的总销量为X份，求X的分布列；
（2）早餐店为了减少浪费，提升利润，决定调整每天制作糕点的份数．
①若产生浪费的概率不超过0.6，求n的最大值；
②以销售这两种糕点的日总利润的期望值为决策依据，在每天所制糕点能全部卖完与n=98之中选其一，应选哪个？
| 甲口味糕点日销量 | 48 | 49 | 50 | 51 |
| 天数 | 20 | 40 | 20 | 20 |
| 乙口味糕点日销量 | 48 | 49 | 50 | 51 |
| 天数 | 40 | 30 | 20 | 10 |
（1）记该店这两种糕点每日的总销量为X份，求X的分布列；
（2）早餐店为了减少浪费，提升利润，决定调整每天制作糕点的份数．
①若产生浪费的概率不超过0.6，求n的最大值；
②以销售这两种糕点的日总利润的期望值为决策依据，在每天所制糕点能全部卖完与n=98之中选其一，应选哪个？
16．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{-x}+a，x≤0}\\{（x-1）^{3}+1，x＞0}\end{array}$，且?x0∈[2，+∞）使得f（-x0）=f（x0），若对任意的x∈R，f（x）＞b恒成立，则实数b的取值范围为（ ）
| A． | （-∞，0） | B． | （-∞，0] | C． | （-∞，a） | D． | （-∞，a] |
15．已知命题p：若a，b是实数，则a＞b是a2＞b2的充分不必要条件；命题q：“?x∈R，x2+2＞3x”的否定是“?x∈R，x2+2＜3x”，则下列命题为真命题的是（ ）
| A． | p∧q | B． | ￢p∧q | C． | p∧￢q | D． | ￢p∧￢q |
14．已知a=log0.50.3，b=log30.5，c=0.50.3，则a，b，c的大小关系是（ ）
0 239180 239188 239194 239198 239204 239206 239210 239216 239218 239224 239230 239234 239236 239240 239246 239248 239254 239258 239260 239264 239266 239270 239272 239274 239275 239276 239278 239279 239280 239282 239284 239288 239290 239294 239296 239300 239306 239308 239314 239318 239320 239324 239330 239336 239338 239344 239348 239350 239356 239360 239366 239374 266669
| A． | a＞c＞b | B． | c＞a＞b | C． | c＞b＞a | D． | b＞c＞a |
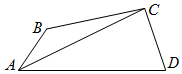如图，在四边形ABCD中，AB=5，BC=7，AC=8，CD=6，BC⊥CD．